| Activitat d’estdistica Bidimensional, mitjana marginal, variància, desviació típica, coeficient de Pearson, recta de regressió, núvol de punts. [Activitat 1]
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 633 › ›
| Activitat d’estdistica Bidimensional, mitjana marginal, variància, desviació típica, coeficient de Pearson, recta de regressió, núvol de punts. [Activitat 2]
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 632 › ›
| Activitat d’estdistica Bidimensional, mitjana marginal, variància, desviació típica, coeficient de Pearson, recta de regressió, núvol de punts. [Activitat 3]
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 631 › ›
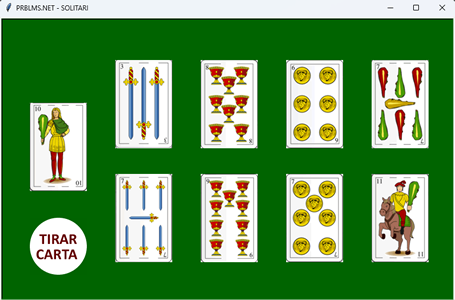
| Aquí tenim un programa fet amb el mòdul Turtle de Python. Aquest programa és un “solitari”, poc usual però prou entretingut.
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 629 › ›
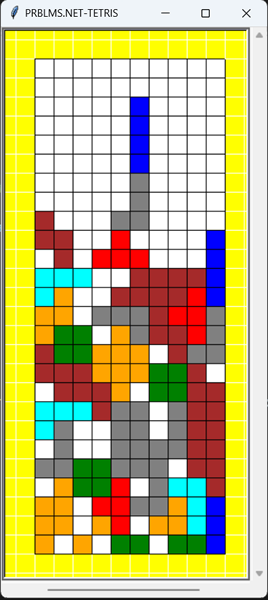
| Aquí tenim un programa fet amb el mòdul Turtle de Python. Aquest programa és un joc força conegut, el TETRIS”
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 628 › ›
| Aquí tenim un programa fet amb el mòdul Turtle de Python. Aquest programa és el joc BUSCAMINES”
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 627 › ›
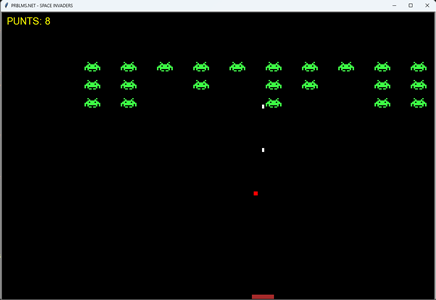
| Aquí tenim un programa fet amb el mòdul Turtle de Python. Aquest programa és el joc SPACE INVADERS”
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 626 › ›
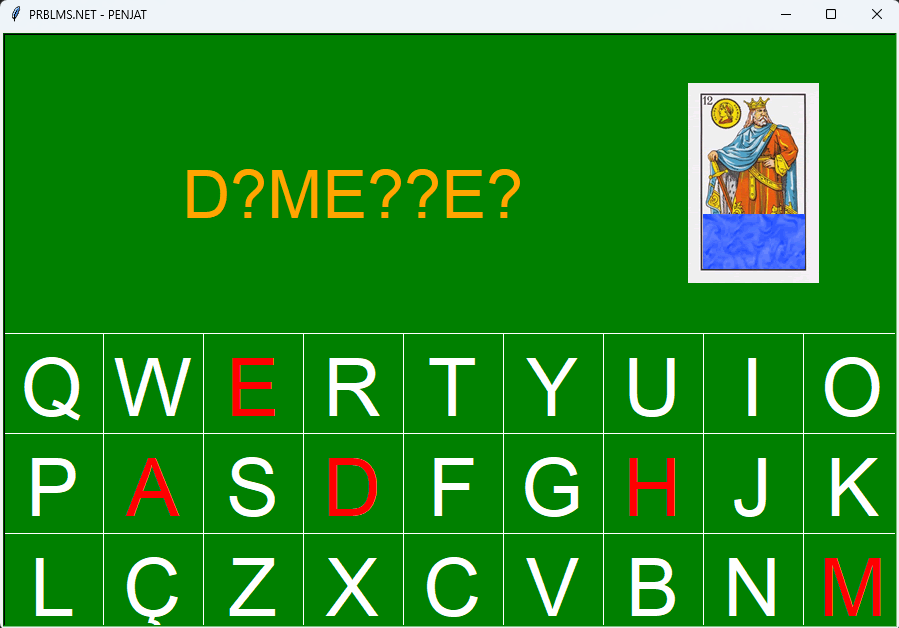
| Aquí tenim un programa fet amb el mòdul Turtle de Python. Aquest programa és el joc del penjat”
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 625 › ›
| En un número de dues xifres, aquestes són consecutives, sent la de les desenes més gran que la de les unitats. Resulta que aquest número és igual a la suma d’aquestes dues xifres multiplicades per 6. Quin número és?
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 624 › ›
| Aquí tenim un programa fet amb el mòdul Turtle de Python. Aquest programa és un jocs pensat per a practicar la mecanografia”
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 623 › ›
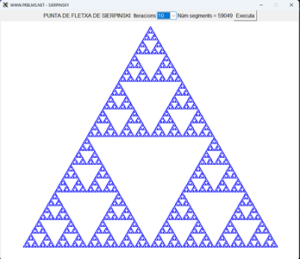
| Aquí tenim un programa fet amb el mòdul Turtle de Python integrat a Tkinter. Aquest programa dibuixa la corba de Sierpinsky amb diferents profunditats. El triangle de Sierpinsky és un fractal que es comenta àmpliament a la Vikipèdia
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 622 › ›
| Aquí tenim un programa fet amb el mòdul Turtle de Python. Aquest programa desenvolupa el conegut joc del PONG però amb dues pales simulant una mena de partit de PING PONG
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 621 › ›
| Aquí tenim un programa fet amb el mòdul Turtle de Python. Aquest programa desenvolupa el conegut joc de l’SNAKE
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 620 › ›
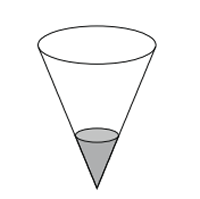
| Un got de forma cònica es posa sota d’una aixeta de la qual en surt aigua amb una velocitat constant. Si ja s’ha omplert fins a la quarta part de la seva altura en un minut, quants minuts passaran des d’aquest moment fins que s’acabi d’omplir?
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 619 › ›
| Aquí tenim un programa fet amb el mòdul Turtle de Python. Aquest programa desenvolupa el conegut joc del MEMORY
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 618 › ›
| La corba de Hilbert es un fractal que es pot dibuixar tal com s’explica a la Vikipèdia.
Aquesta aplicació en Python dibuixa la corba en 8 diferents nivells d’iteració a la nostra elecció per a obtenir una imatge com la que veiem a la dreta.
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 617 › ›
| El Triangle de Sierpinski es un fractal que es pot dibuixar amb el “Joc del Caos” tal com s’explica a la Vikipèdia
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 616 › ›
La Catifa de Sierpinski es un fractal descrit a prinicpis del s XX pel matemàtic polonès W. Sierpinski.
Aqui incorporem una apliacació feta amb Python amb el mòdul Turtle que dibuixa aquesta figura.Entrada a la Vikipèdia |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 615 › ›
| Els catets dels triangles mesuren 1 cm, quan valen les àrees acolorides? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 614 › ›
|
|

























