El domador amb més experiència d’un circ necessita 40 minuts per rentar un elefant. El seu fill, que n’està aprenent, completa la mateixa feina en 2 hores.
Quant de temps trigaran, treballant tots dos junts, a netejar els tres elefants que té el circ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 571 › ›
Dues aixetes A i B omplen una piscina en 2 h. L’aixeta A, ella sola, triga a omplir-la 3h menys que l’aixeta B, ella sola.
Quant triga cada aixeta per si sola a omplir la piscina? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 551 › ›
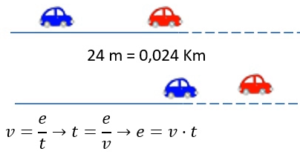
Dos cotxes circulen per una carretera a una velocitat de 80 km/h i mantenen entre si una distància constant de 24 m. En un cert punt entren en una carretera secundària i tots dos passen a circular a una velocitat de 50 km/h.
Quina és la distància que separa aleshores els dos cotxes? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 546 › ›
De la llista de n nombres 1, 2, 3, . . . , n se n’elimina un. La mitjana aritmètica dels nombres restants és 4,75.
Quin és el nombre que s’ha eliminat? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 532 › ›
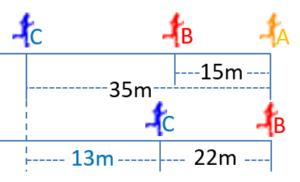
| L’Anna, en Bernat i en Carles corren una cursa. Surten junts i cadascú manté una velocitat constant. Quan l’Anna arriba al final, a en Bernat li falten 15 m per a acabar, i a en Carles, 35 m.
Quan en Bernat acaba, a en Carles li queden 22 m.
Quina és la longitud de la cursa? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 530 › ›
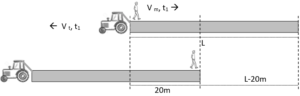
| En Marc va veure un tractor que arrossegava, a velocitat constant, un tub. Per tal de deduir quina era la longitud del tub, en Marc es va posar a caminar, també a velocitat constant, pel costat del tub. Primer va caminar en sentit contrari al del tractor i va haver de fer 20 passes per a anar d’una punta a l’altra. Després va caminar al costat del tub però en el mateix sentit que el tractor i va haver de fer 140 passes per a anar d’una punta a l’altra. Sabent que en Marc fa les passes d’1 m, quina és la longitud del tub? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 525 › ›
| Els autobusos d’un aeroport surten cada 3 minuts cap al centre de la ciutat. Van per un carril reservat i tarden 35 minuts a arribar al centre. Un cotxe surt de l’aeroport al mateix temps que un autobús cap al centre i fa el mateix recorregut que el autobús però tarda 60 minuts. Sense comptar l’autobús que ha sortit al mateix temps que el cotxe, quants autobusos l’avançaran en el trajecte cap al centre? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 522 › ›
| Es vol fer una mescla dels colors blau i groc en la següent proporció: 3 litres de color groc i 2 litres de color blau. Per error es posen les quantitats a l’inrevés, o sigui 3 litres de color blau i 2 litres de color groc.
Quants litres de la mescla cal llençar i substituir per la mateixa quantitat de color groc per a obtenir la mescla desitjada inicialment? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 509 › ›
Problema proposat per Einstein. Condicions inicials:
– Tenim cinc cases, cadascuna d’un color.
– Cada casa té un amo de nacionalitat diferent.
– Els 5 amos beuen una beguda diferent, fumen marca diferent i tenen mascota diferent.
– Cap amo té la mateixa mascota, fuma el mateix o beu el mateix que un altre.
Dades:
1. El noruec viu a la primera casa, al costat de la casa blava.
2. El qui viu a la casa de centre pren llet.
3. L’anglès viu a la casa vermella.
4. La mascota del suec és un gos.
5. El danès beu te.
6. La casa verda és la immediata de l’esquerra de la casa blanca.
7. El de la casa verda beu cafè.
8. El que fuma PM cria ocells.
9. El de la casa groga fuma Dunhill.
10. El que fuma Blend viu al costat del què té gats.
11. El que té cavalls viu al costat de què fuma Dunhill.
12. El que fuma Blue beu cervesa.
13. L’alemany fuma Prince.
14. El que fuma Blend té un veí que beu aigua.
Qui té peixos per mascota? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 422 › ›
| Diofant va ser un matemàtic grec de l’escola d’Alexandria (s.IV d.C.). Va estudiar la resolució d’equacions i, especialment, va ser un innovador en la seva teoria d’equacions de primer i segon graus. Però sabem poc de la seva vida. Tot el que es coneix sobre ell ha estat pres de la dedicatòria que figura al seu sepulcre, inscripció composta en forma d’exercici matemàtic, que reproduïm a continuació:
¡Caminant! Aquí van ser sepultats les restes de Diofant. I els números poden mostrar, oh, miracle! com de llarga va ser la seva vida, la sisena part va constituir la seva bella infància. Hi havia transcorregut a més una dotzena part de la seva vida, quan de borrissol es va cobrir la seva barbeta. I després la setena part de la seva existència va transcórrer en un matrimoni estèril. Va passar un quinquenni més i li va fer feliç el naixement del seu preciós primogènit, qui va lliurar el seu cos, la seva bella existència, que va durar tan sols la meitat de la del seu pare a la terra. I amb profunda pena va descendir a la sepultura, havent sobreviscut quatre anys al seu estimat fill.
Es tracta d’esbrinar quants anys va viure Diofant, a quina edat es va casar, quan va tenir el seu primer fill i a quina edat el va perdre. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 418 › ›
| Quina hora és si perquè acabi el dia falten quatre hores menys de les que han passat? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 413 › ›
| En Lluís un matemàtic es troba a l’Anna una companya de facultat que fa temps que no es veien i…
Lluís: Hola Anna, quant temps sense veure’ns, com et va la vida?
Anna: Prou bé, ja tinc tres fills
Lluís: Ah què bé! I quants anys tenen?
Anna: Doncs guaita, a veure si les saps dir, la suma de les seves edats dóna 13
Lluís: Dona, amb això no en tinc prou!
Anna: Tens raó, et dono més informació, el producte de les seves edats coincideix amb la nostra
Lluís: Mmmm …, encara em falten dades
Anna: És veritat, el gran estudia piano.
Lluís: Mmmm…, ara sí. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 402 › ›
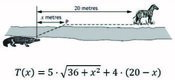
Un cocodril vol capturar una zebra que està 20m més endavant però a l’altra banda del riu. El cocodril viatja a diferent velocitat a l’aigua i a terra. El temps que triga el cocodril en atrapar la zebra ve donat per la fórmula de la dreta.
Estudia 3 situacions:
1 – El cocodril no viatja per terra i segueix una línia recta a través del riu fins a atrapar-la
2 – El cocodril viatja, per l’aigua, la distància més curta possible
3 – Entre els temps que s’han obtingut en els casos anteriors hi ha un valor de x que minimitza el temps que triga el cocodril en atrapar la presa. Troba’l i digues quin és aquest temps. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 310 › ›
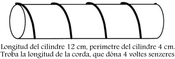
| Troba la longitud d’una corda que dóna 4 voltes senceres a un cilindre de 12 cm de longitud i 4 cm de perímetre |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 309 › ›
|
|