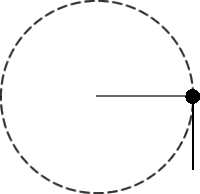
[PAAU 2004] Una partícula de massa 0,1 kg, lligada a l’extrem d’un fil, descriu un moviment circular en un pla vertical. Quan el fil es troba en posició horitzontal, la seva tensió és 10 N. Calcula per a aquesta posició:
a) L’acceleració centrípeta de la partícula.
b) L’acceleració tangencial de la partícula |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 175 › ›
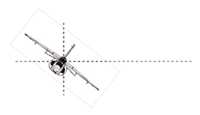
[PAAU 2004] Un avió vola a una velocitat de mòdul 400 m/s, constant, i descriu un cercle en un pla horitzontal. Els límits de seguretat li permeten experimentar com a màxim una acceleració que és vuit vegades la de la gravetat. En aquestes condicions extremes, calcula:
a) El radi de la trajectòria circular.
b) El temps que l’avió triga a fer una volta.
c) L’angle d’inclinació de les ales de l’avió respecte de l’horitzontal perquè la força de sustentació (perpendicular al pla definit per les ales) li permeti fer aquest gir. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 174 › ›
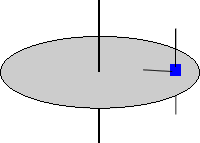
| [PAAU 2008] Una plataforma circular gira, en un pla horitzontal, respecte d’un eix vertical que passa pel seu centre, a una velocitat de 120/π rpm (revolucions per minut). Determineu el valor de la distància màxima respecte de l’eix a què pot situar-se una massa sobre la plataforma de manera que giri solidàriament amb aquesta, sense lliscar, sabent que el coeficient de fregament estàtic val 0,5. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 173 › ›
[PAAU 2009] Una atracció d’una fira consisteix en uns cotxes petits que giren a una velocitat de mòdul constant de 3,0 m/s i que descriuen una circumferència de 8,0 m de radi en un pla horitzontal.
a) Calculeu les components intrínseques de l’acceleració d’un dels cotxes.
b) Si el mòdul de la velocitat dels cotxes, quan finalitza el temps de l’atracció, es redueix de manera uniforme des de 3,0 m/s fins a 1,0 m/s en 10 s, calculeu-ne l’acceleració angular i l’acceleració tangencial en aquest interval de temps. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 154 › ›
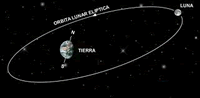
| [PAAU 2004] La Lluna descriu una òrbita al voltant de la Terra que correspon pràcticament a un moviment circular uniforme de període T= 27,4 dies. La llum procedent de la Lluna triga 1,28 s a arribar a la Terra.
Calcula la velocitat angular i l’acceleració de la Lluna. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 142 › ›
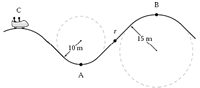
Un cotxe d’una muntanya russa està fent el recorregut que veiem a la imatge. Si la seva velocitat és constant i de valor 8 m/s i la seva massa amb els passatgers és de 600 Kg. Indica
a) Quin és el pes aparent en el punt més baix del recorregut?
b) Quin és el pes aparent en el punt més alt del recorregut? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 128 › ›
| Un vehicle de massa 1200 Kg circula per un turonet, que podem suposar que té la forma d’un arc de circumferència de radi 11 m. Quina és la màxima velocitat a que pot anar sense perdre contacte amb la superfície? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 127 › ›
En un dia assolejat, un cotxe de massa 1500 Kg dóna voltes en un circuït circular sense peraltar de radi 35 m. Si el coeficient de fregament de les rodes amb el terra sec és de 0,5 indica
a) La velocitat màxima a la que pot circular sense sortir-se de la pista
En un dia que el circuït és moll, amb una v=8 m/s el cotxe comença a derrapar
b) Quin és el coeficient de fregament en aquestes condicions.
Repeteix el problema però suposant que ara circula una motocicleta de massa 200 Kg. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 126 › ›
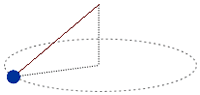
Fem girar una bola de massa 0,5 Kg, unida a una corda de 1,5 m segons l’esquema. Si la tensió màxima que pot suportar la corda és de 50 N. Calculeu:
a) L’angle de gir amb la tensió màxima.
b) La velocitat de la bola amb la tensió màxima. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 125 › ›
| Quina velocitat mínima ha de portar un ciclista que vol fer el ris de la mort en una pista de radi 10 m? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 124 › ›
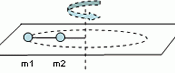
| Dues boles de masses m1= 4 Kg i m2= 3 Kg, giren amb radis respectius R1= 3 m i R2= 2 m. La velocitat angular és de 5 rad/s i és constant. Calculeu les tensions de les cordes i les acceleracions de cada cos. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 109 › ›
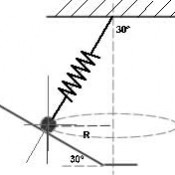
Un peralt té una molla comprimida que exerceix una pressió contra un cos de massa 10 Kg. L’angle del peralt amb l’horitzontal i l’angle de la molla amb la vertical son iguals i de 30º. (Hooke)
No hi ha fricció i la velocitat angular val 2 rad/s. La constant de la molla val 250 N/m.
a) Calculeu el radi de rotació
b) Calculeu la força centrípeta
c) Calculeu la força que fa la molla |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 108 › ›
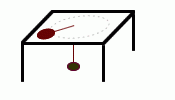
[PAAU 1997] Una massa d’1 Kg. situada sobre una taula que no presenta fregament s’uneix a una altra massa de 4 Kg mitjançant una corda que passa per un forat fet al mig de la taula. El cos de 4 Kg està en repòs, mentre que el cos d’1 Kg descriu un moviment circular uniforme amb un radi de 0,1 m.
a) Feu un esquema amb les forces que actuen sobre cada cos i especifiqueu-hi les relacions entre elles.
b) Calculeu la velocitat amb què es mou el cos de massa 1 Kg.
c) Indiqueu quines són les acceleracions tangencials i normals del cos de massa 1 Kg. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 54 › ›
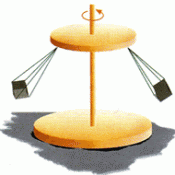
[PAAU 2004] El muntatge d’una atracció de fira consisteix en una anella horitzontal de 3 m de radi de la qual pengen cordes de 4m de longitud i a l’extrem de les quals hi ha una cadireta de massa 2 Kg. L’anella gira a una velocitat angular constant al voltant d’un eix vertical que passa pel seu centre.
a) Calculeu la velocitat angular de l’anella quan la corda forma un angle de 37º amb la vertical
b) En les condicions anteriors calculeu la tensió a la que està sotmesa la corda
c) Si la tensió màxima que pot suportar la corda és de 796 N i l’angle a la que gira l’atracció seguix sent 37º, quina és la massa màxima que pot tenir un usuari d’aquesta atracció? (g=9,8 m/s²) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 50 › ›
| Quina velocitat angular s’ha de donar a una estació espacial de forma anular de 60 m de diàmetre per tal de crear una gravetat artificial igual a la terrestre? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 39 › ›
Una centrifugadora de 12 cm de radi que està inicialment en repòs, accelera uniformement durant 20 s. En aquest interval de temps, acceleració tangencial=100·Π rad/s². Després manté constant la velocitat adquirida.
a) Amb quina velocitat gira la centrifugadora quan fa 20 s que funciona? Expresseu el resultat en RPM
b) Quantes voltes ha ha fet la centrifugadora després de funcionar durant 20 s? I després de funcionar 50 s?
c) Calculeu les acceleracions tangencial i normal que tenen els objectes a l’interior de la centrifugadora quan aquesta fa 1 minut que gira |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 20 › ›
| Són les 12 en punt. Tant la busca horària com la minutera del rellotge apunten cap amunt.
En quin moment tornaran a coincidir per primer cop l’una sobre l’altra? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 19 › ›
| Un cotxe es mou per una carretera seguint una corba amb una velocitat constant de 60 Km/h.
Té acceleració el cotxe? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 18 › ›
|
|


























