Un cotxe de massa 1.250 kg descriu un revolt circular, no peraltat, de 300 m de radi. La trajectòria és mitja circumferència. El cotxe augmenta de velocitat de manera uniforme mentre descriu el revolt, i passa d’anar a 40 km/h a l’inici a anar a 80 km/h al final. Calcula:
a) L’acceleració tangencial i l’acceleració centrípeta que té el cotxe quan circula a 20 m/s pel revolt.
b) El valor de la força de fricció estàtica entre les rodes i l’asfalt quan el cotxe circula a 20 m/s.
c) El valor del coeficient de fricció estàtica entre les rodes i l’asfalt si el cotxe pot circular pel revolt a una velocitat màxima de 30 m/s sense derrapar. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 177 › ›
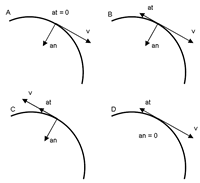
| [PAAU 2004] Considera una partícula que descriu un moviment circular uniformement retardat, amb acceleració angular no nul·la. Quin dels diagrames següents li correspon? Tria la resposta que consideris correcta i justifica la resposta. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 171 › ›
[PAAU 2009] Una atracció d’una fira consisteix en uns cotxes petits que giren a una velocitat de mòdul constant de 3,0 m/s i que descriuen una circumferència de 8,0 m de radi en un pla horitzontal.
a) Calculeu les components intrínseques de l’acceleració d’un dels cotxes.
b) Si el mòdul de la velocitat dels cotxes, quan finalitza el temps de l’atracció, es redueix de manera uniforme des de 3,0 m/s fins a 1,0 m/s en 10 s, calculeu-ne l’acceleració angular i l’acceleració tangencial en aquest interval de temps. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 154 › ›
[PAAU 2006] Un disc es posa a girar des del repòs. En els primers 40 s augmenta la seva velocitat angular de manera uniforme i gira 10 voltes senceres.
Calculeu les components intrínseques (normal i tangencial) del vector acceleració per a un punt del disc situat a 15 cm del seu centre, quan fa 15 s que s’ha iniciat el moviment. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 153 › ›
[PAAU 2005] Una roda de 3 m de radi realitza un moviment circular uniformement accelerat amb una acceleració angular de 2 rad/s², partint del repòs
a) En un mateix instant, tots els punts de la roda tenen la mateixa:
1) Velocitat lineal.
2) Velocitat angular.
3) Acceleració normal.
b. L’acceleració tangencial:
1) Augmenta amb el temps.
2) Augmenta amb la distància al centre.
3) És la mateixa per a tots els punts de la roda.
c. L’acceleració normal:
1) No depèn del temps.
2) És la mateixa per a tots els punts de la roda.
3) Va dirigida cap al centre.
d) Passats 2 s, els punts de la perifèria tenen una velocitat lineal de:
1) 12 rad/s.
2) 12 m/s.
3) 4 m/s. e. En aquests 2 s, la roda ha girat:
1) Menys d’una volta.
2) Més d’una volta.
3) Exactament una volta. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 152 › ›
[PAAU 2001] Un mòbil que surt del repòs segueix una trajectòria circular de 3 m de radi amb una acceleració angular constant de Π rad/s²
a) Quant temps triga a fer una volta completa? Quina és la longitud de l’arc recorregut durant la meitat d’aquest temps?
b) Quina és la velocitat angular del mòbil a l’instant t= 0,5 s? I l’acceleració normal al mateix instant?
c) Quant val l’acceleració tangencial del mòbil a l’instant t= 0,5 s? Quin angle formen l’acceleració tangencial i l’acceleració normal en aquest instant? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 151 › ›
| [PAAU 2002] El mòdul de la velocitat d’un punt material que descriu una trajectòria circular ve donat per l’equació (en unitats del SI) v= 6+10t. Si el radi de la trajectòria és de 100 m, quina serà l’acceleració normal en l’instant t= 8s. I l’acceleració tangencial? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 149 › ›
[PAAU 2004] En un moviment circular de radi r= 6.5 m, la velocitat angular ve donada per l’expressió ->2 + 3t (unitats SI)
a) Es tracta d’un MCUA? Per què?
b) Calcula l’acceleració tangencial i l’acceleració normal del punt mòbil en l’instant t= 3 s
c) Determina la longitud de l’arc recorregut en els dos primers segons del moviment
d) Troba la velocitat que agafa al final de la 1a volta |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 148 › ›
[PAAU 2002] Un mòbil que surt del repòs realitza un moviment circular accelerat uniformement. Raoneu si cadascuna de les afirmacions següents és certa o falsa:
a) El valor de l’acceleració normal del mòbil augmenta amb el temps
b) El valor de l’acceleració tangencial del mòbil no varia amb el temps |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 146 › ›
| [PAAU 1998] En un moviment curvilini l’acceleració forma, en un moment donat, un angle de 60º amb la velocitat i val 6 m/s². Calcula, per quest instant, el mòdul de les acceleracions tangencial i normal |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 145 › ›
| [PAAU 2001] Una partícula segueix una trajectòria circular de 3 m de radi. Si l’angle descrit ve donat per l’equació: angle= t² -1 on l’angle està expressat en radians i t en segons, quina és la longitud de l’arc recorregut entre els instants t= 1 s i t= 3 s? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 144 › ›
[PAAU 2003] Una partícula segueix una trajectòria circular. Si l’angle descrit en funció del temps ve donat per l’expressió α= t², (en unitats del SI) calcula:
a) El temps que triga la partícula a fer les dues primeres voltes.
b) La velocitat angular de la partícula a t= s. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 141 › ›
[PAAU 1999] Un mòbil descriu un moviment circular de radi 2m. L’angle descrit pel mòbil en funció del temps ve donat per l’equació t³ + 5t – 4 (en unitats del SI). Calcula la expressió de la velocitat angular i l’acceleració tangencial per t=1s.
[Aquest és un Moviment Circular NO Uniformement Accelerat] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 140 › ›
| [PAAU 2002] El mòdul de la velocitat d’un punt material que descriu una trajectòria circular ve donat per l’equació (en unitats del SI) v=6 + 10t. Si el radi de la trajectòria és de 100 m, quina serà l’acceleració normal quan t= 8 s? I l’acceleració tangencial? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 138 › ›
| Una partícula que parteix del repòs descriu un moviment circular uniformement accelerat. Calculeu l’angle que ha girat en el moment en que els mòduls de l’acceleració tangencial és el doble que el mòdul de l’acceleració normal |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 42 › ›
Un automòbil circula a 80 Km/h, frena i s’atura en 10 s. Calculeu
a) Les voltes que faran les rodes si tenen un radi de 50 cm.
b) L’acceleració angular de les rodes |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 41 › ›
Una roda de radi 20 cm, partint del repòs gira amb una acceleració angular constant i al cap de 5 s té una velocitat angular de 300 RPM, es demana:
Velocitat angular en rad/s, Velocitat lineal dels punts de la superfície de la roda, Acceleració angular, Acceleració angular, Acceleració tangencial, Acceleració normal, Acceleració total, Angle girat i Espai recorregut en girar la roda. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 24 › ›
La velocitat angular d’una roda passa de 1000 RPM a 750 RPM en 10 s. És demana:
a) L’acceleració angular
b) El nombre de voltes que fa en aquests 10 s. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 22 › ›
Una centrifugadora de 12 cm de radi que està inicialment en repòs, accelera uniformement durant 20 s. En aquest interval de temps, acceleració tangencial=100·Π rad/s². Després manté constant la velocitat adquirida.
a) Amb quina velocitat gira la centrifugadora quan fa 20 s que funciona? Expresseu el resultat en RPM
b) Quantes voltes ha ha fet la centrifugadora després de funcionar durant 20 s? I després de funcionar 50 s?
c) Calculeu les acceleracions tangencial i normal que tenen els objectes a l’interior de la centrifugadora quan aquesta fa 1 minut que gira |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 20 › ›
|
|
















