Un noi te una pilota a la mà, a l’alçada d’1 m. La llença verticalment amb una velocitat inicial de 20 m/s. (Considereu g= 10 m/s²)
1) Troba al cap de quant temps després de llençar la pilota, aquesta assolirà l’altura màxima
2) Quina serà l’altura màxima assolida
3) En quin instant arribarà la pilota al terra |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 236 › ›
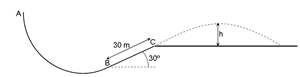
[PAAU 1999] Un esquiador de 80 kg que surt des de A arriba a B amb una velocitat de 30 m/s, i quan passa per C la seva velocitat és de 23 m/s. La distància entre B i C és de 30 m.
a) Quant han variat les energies cinètica i potencial de l’esquiador en anar des de B fins a C?
b) Quanta energia s’ha perdut per fregament en el tram recte BC? Quant val la força de fregament, suposada constant, en aquest tram?
c) Si la pista s’acaba a C i l’esquiador fa un salt parabòlic, quina és la màxima alçada h que assolirà, mesurada sobre el nivell de C (observa el dibuix)?
Suposa negligibles els efectes del fregament amb l’aire. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 193 › ›
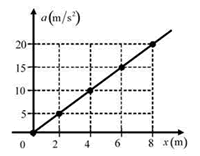
| [PAAU 2008] En la gràfica següent es mostra com varia l’acceleració d’un cos de massa 10 kg que es mou en línia recta. Quin treball s’ha efectuat sobre el cos per a moure’l des de x = 0 fins a x = 8 m? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 190 › ›
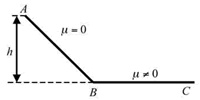
[PAAU 2009] El punt més alt d’una pista d’esquí (que podem aproximar a un pla inclinat sense fregament, tram AB), es troba a una altura h respecte del final. Fora de la pista, tram BC, no queda neu i per tant hi ha fregament (coeficient de fregament, μ, no nul). Si un esquiador surt del començament de la pista (punt A) a una velocitat nul·la:
1) Quina serà la seva velocitat al final de la pista (punt B)?
a) ARREL(2gh)
b) ARREL(gh/2)
c) Depèn de la massa de l’esquiador.
2) Quina distància horitzontal (BC) recorrerà l’esquiador abans d’aturar-se?
a) h·ARREL(μ)
b) h·μ
c) h/μ |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 188 › ›
[PAAU 2003] Una massa de 5 kg està penjada d’un fil vertical, inextensible i de massa negligible. Si la tensió del fil té un valor de 60 N, raona quina de les propostes següents és correcta:
a) La massa puja a velocitat constant.
b) La massa té una acceleració cap amunt de 2 m/s².
c) La massa es troba en repòs.
Considera g = 10 m/s². |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 158 › ›
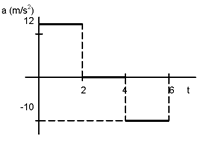
| [PAAU 2001] Una partícula surt del repòs i es mou sobre una recta. A la gràfica adjunta es representa l’acceleració de la partícula durant els 6 primers segons. Representa la gràfica v(t) del moviment |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 150 › ›
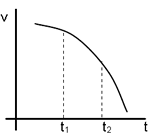
[PAAU 1998] El gràfic del costat està referit a un mòbil que descriu un moviment rectilini. Raona si les afirmacions següents són vertaderes o falses:
a) La gràfica correspon a un moviment uniformement accelerat
b) L’acceleració en el punt t1 és positiva i en el punt t2 és negativa |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 147 › ›
[PAAU 2000] Des d’una altura de 200 m sobre el terra llancem verticalment i cap amunt un cos amb una velocitat de 30 m/s.
a) Quant temps trigarà a recórrer els darrers 50 m?
b) Quina serà la seva posició respecte al terra a l’instant en que el cos baixa amb una velocitat de mòdul 40 m/s?
c) Feu un dibuix aproximat de la gràfica velocitat-temps corresponent al moviment d’aquest cos des de l’instant del llançament fins que arriba a terra.
Considereu g= 10 m/s² |
› › Clica per a veure el vídeo d’ACTIVITAT 143 › ›
| Les dades de la taula corresponen a un cos que es mou amb MRUA. Acaba-la d’omplir |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 139 › ›
| [PAAU 1999] El rècord del món de salt d’altura està en 2,45 m. Es demana quina ha estat la velocitat inicial que ha fet l’atleta al iniciar el salt. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 137 › ›
| [PAAU 1999] D’una aixeta gotegen separades l’una de l’altra, dues gotes d’aigua. En un instant determinat, estan separades una distància d. Raona si, amb el pas del temps, mentre cauen, aquesta distància anirà augmentant, minvant o romandrà constant |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 136 › ›
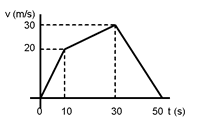
[PAAU 2001] La gràfica de la figura representa la velocitat en funció del temps d’un mòbil que surt de l’origen de coordenades i segueix un moviment rectilini. Calcula:
a) L’acceleració del mòbil a l’instant t= 20 s
b) La distància recorreguda durant el moviment de frenada
c) En quin interval de temps la seva acceleració és màxima? Dibuixa la gràfica x(t) per aquest interval |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 135 › ›
Dos mòbils es mouen seguint una trajectòria rectilínia entre els punts A i B situats a 500 m l’un de l’altre. El primer surt d’A a una Vi=10 m/s i va cap a B amb una acceleració constant on arriba a una Vf=50 m/s. El vehicle que surt de B cap a A va a una velocitat constant de 20 m/s i comença el seu recorregut 3 segons més tard.
a) Quina acceleració té el mòbil A?
b) En quin punt es trobaran?
c) En quin punt està el mòbil que surt d’A en el moment que té la mateixa velocitat que el mòbil B? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 130 › ›
Un ascensor de massa 1600 Kg puja des de la planta baixa d’un edifici fins a la 3a que es troba a 9 m d’altura. Arrenca des del repòs de manera que durant els 1,1 primers segons es mou amb MRUA i assoleix una altura de 1,15 m. Continua amb velocitat constant fins arribar als 7,85 m i a partir d’aquest punt frena durant 1,1 s fins a aturar-se al 3r pis.
Determineu el treball i la potència desenvolupats per la maquinaria del ascensor en els tres trams del recorregut. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 88 › ›
Un motorista es troba inicialment aturat en un semàfor i arrenca amb una acceleració de 1,5 m/s², movent-se en línia recta. En el mateix moment un automòbil que es mou en sentit contrari es troba a una distància de 2 Km del motorista, amb una velocitat constant de 108 Km/h
a) Calculeu al cap de quant temps es troben
b) Calculeu a quina distància del semàfor es troben |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 14 › ›
El temps dels primers classificats de la final olímpica d’una cursa de natació és: medalla d’or: 47,14 s i medalla de plata: 47,5 s. Sabem que tota la cursa va amb MRUA i l’acceleració del medalla d’or és de 0,09 m/s².
a) Quina és la longitud de la prova?
b) Amb quina acceleració neda el 2n classificat? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 13 › ›
Dos mòbils es mouen seguint una trajectòria rectilínia entre els punts A i B situats a 500 m l’un de l’altre. El primer surt d’A a una Vi=10 m/s i va cap a B amb una acceleració constant on arriba a una Vf=50 m/s. El vehicle que surt de B cap a A va a una velocitat constant de 20 m/s.
a) Quina acceleració té el mòbil A?
b) En quin punt es trobaran?
c) En quin punt està el mòbil que surt d’A en el moment que té la mateixa velocitat que el mòbil B? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 11 › ›
Una motocicleta, partint del repòs fa un recorregut d’1 Km en 31,8 s. Si el moviment és rectilini uniformement accelerat (MRUA).
a) Calculeu l’acceleració
b) Calculeu la velocitat final. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 8 › ›
Un avió necessita una velocitat de 360 km/h per a enlairar-se; si partint del repòs triga 25 s en aixecar el vol, es demana:
a) A quina acceleració està sotmès l’avió?
b) Quina longitud recorre abans d’enlairar-se? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 1 › ›
|
|

























