| [PAAU 2010] Donada la matriu de la imatge a) Calculeu A² i A³ b) Deduïu el valor de A101 |
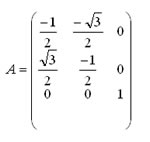 |
|
||||||||||||||||||||
|
||||||||||||||||||||
|
Copyright © 2025 PRoBLeMeS - email:correu@prblms.net Powered by WordPress & Atahualpa |
||||||||||||||||||||
|
||||||||||||||||||||||
|
||||||||||||||||||||||
|
Copyright © 2025 PRoBLeMeS - email:correu@prblms.net Powered by WordPress & Atahualpa |
||||||||||||||||||||||