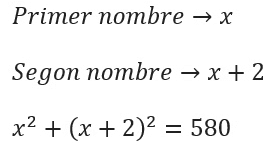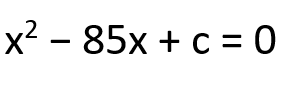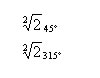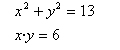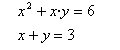Dos números naturals tenen una diferència de dues unitats i la suma dels seus quadrats és 580.
Quins números són? |
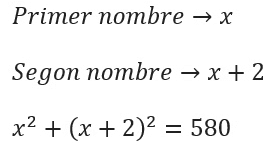 |
› › Clica per a veure el vídeo d’ACTIVITAT 553 › ›
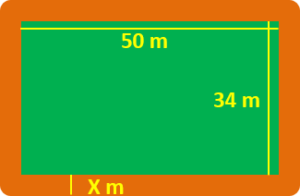
| Un jardí rectangular de 50m de llarg i 34 d’ample està envoltat per un camí.
Troba l’amplada d’aquest camí si se sap que la seva àrea es de 172 m2. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 552 › ›
Dues aixetes A i B omplen una piscina en 2 h. L’aixeta A, ella sola, triga a omplir-la 3h menys que l’aixeta B, ella sola.
Quant triga cada aixeta per si sola a omplir la piscina? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 551 › ›
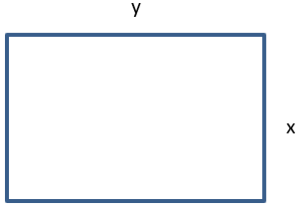
Per a tancar una finca rectangular de 875 m2 s’han fet servir 120 m de tanca.
Calcula las dimensiones de la finca. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 550 › ›
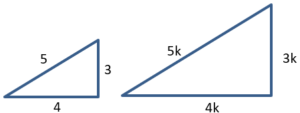
Els tres costats d’un triangle són proporcionals als d’un altre triangle de valors 3, 4, 5.
Troba els costats d’aquest triangle sabent que la seva àrea és de 54 m2. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 549 › ›
| Si les dues solucions de l’equació x2 − 85x + c = 0 són nombres primers…
Quant val c? |
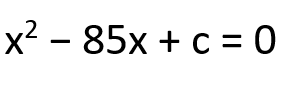 |
› › Clica per a veure el vídeo d’ACTIVITAT 539 › ›
| Un conill i un eriçó van participar en una cursa per una pista circular de 550 m de llargada, on coincideixen la sortida i l’arribada. La velocitat del conill era de 10 m/s i la de l’eriçó d’1 m/s. Van començar simultàniament. Però l’eriçó, amb ganes d’enganyar, va començar en la direcció contrària a la que corria el conill. Quan es van trobar, l’eriçó va girar cua immediatament i va córrer darrere del conill. Quant de temps després del conill va arribar l’eriçó a la meta? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 502 › ›
| Una llebre i una tortuga competeixen en una cursa de 5 km al llarg d’una línia recta. La llebre és cinc vegades més ràpida que la tortuga. Per error, la llebre ha començat la cursa en direcció perpendicular a la línia fixada. Al cap d’una estona s’ha adonat del seu error, ha corregit la seva direcció i s’ha dirigit en línia recta cap al punt d’arribada. Ha arribat al mateix temps que la tortuga. Quina és la distància entre el punt on la llebre ha girat i el punt d’arribada? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 479 › ›
Representa la paràbola (Y – 3)2 = – 4(X + 2), trobant els elements d’interès de la figura i la seva expressió general
› › Clica per a veure el vídeo d’ACTIVITAT 399 › ›
Donada l’equació 5x2 – 3x + 2 =0, que té per solucions p i q. Troba l’equació que té per solucions els seus quadrats, o sigui p2 i q2.
› › Clica per a veure el vídeo d’ACTIVITAT 375 › ›
Donada l’equació 5x2 – 3x + 2 =0, que té per solucions p i q. Troba l’equació que té per solucions els seus inversos, o sigui 1/p i 1/q.
› › Clica per a veure el vídeo d’ACTIVITAT 374 › ›
[IBO] Troba els valors que pot tenir k, perquè les solucions a i b de l’equació x² – kx + (k+1) = 0, compleixin que a² + b² = 13
› › Clica per a veure el vídeo d’ACTIVITAT 361 › ›
[IBO] Troba els valors de k que fan que l’equació (1+2k)x² -10x +k-2=0 tingui solucions reals
› › Clica per a veure el vídeo d’ACTIVITAT 353 › ›
| [IBO] Les arrels de l’equació 2x² + 4x – 1 = 0 són a i b (no calculis l’arrel).
Quina és l’equació de 2n grau que té com a solucions a² i b²? |
|
› › Clica per a veure el vídeo d’ACTIVITAT 318 › ›
| Troba una equació de segon grau que tingui per solucions els números complexos que veus indicats a la pantalla |
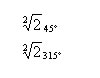 |
› › Clica per a veure el vídeo d’ACTIVITAT 244 › ›
Un noi te una pilota a la mà, a l’alçada d’1 m. La llença verticalment amb una velocitat inicial de 20 m/s. (Considereu g= 10 m/s²)
1) Troba al cap de quant temps després de llençar la pilota, aquesta assolirà l’altura màxima
2) Quina serà l’altura màxima assolida
3) En quin instant arribarà la pilota al terra |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 236 › ›
La funció de 2n grau – Aplicació de Geogebra
Amb aquesta aplicació es pot estudiar el comportament de la funció de 2n grau.
Es pot veure com evoluciona la seva forma, eix de simetria; les arrels, el punt de tall amb l’eix d’ordenades, vèrtex, i eventualment el màxim / mínim; tot depenent dels coeficients.
› › Clica per a veure el vídeo d’ACTIVITAT 233 › ›
Troba el valor de la constant k perquè:
a) L’equació tingui 2 solucions
b) L’equació tingui 1 solució
c) L’equació no tingui solucions |
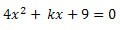 |
› › Clica per a veure el vídeo d’ACTIVITAT 199 › ›
| Resol el sistema de dues equacions de segon grau amb dues incògnites al quadrat de la imatge |
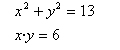 |
› › Clica per a veure el vídeo d’ACTIVITAT 197 › ›
| Resol el sistema de dues equacions de segon grau amb dues incògnites al quadrat de la imatge |
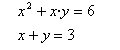 |
› › Clica per a veure el vídeo d’ACTIVITAT 196 › ›
|
|