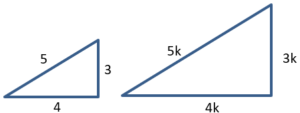
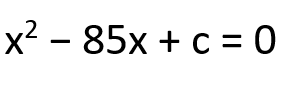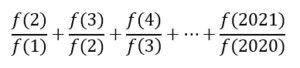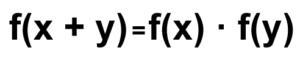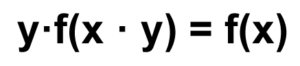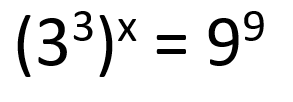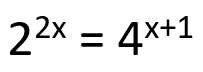Els tres costats d’un triangle són proporcionals als d’un altre triangle de valors 3, 4, 5.
Troba els costats d’aquest triangle sabent que la seva àrea és de 54 m2. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 549 › ›
| Si les dues solucions de l’equació x2 − 85x + c = 0 són nombres primers…
Quant val c? |
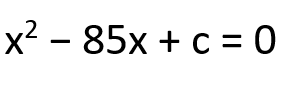 |
› › Clica per a veure el vídeo d’ACTIVITAT 539 › ›
| D’aquí a dos anys el meu fill serà dues vegades més gran que era fa dos anys. I la meva filla serà d’aquí a tres anys tres vegades més gran que era fa tres anys.
Qui és més gran, el nen o la nena? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 537 › ›
| El meu fill és ara 3 vegades més jove que jo. Però fa 5 anys era 4 vegades més jove. Quants anys té? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 536 › ›
| El meu germà gran em porta 8 anys.
Dins de quants anys la seva edat serà el doble de la meva, si fa 3 anys era el triple? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 535 › ›
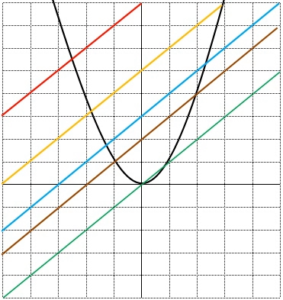
| En acabar la classe de matemàtiques ha quedat dibuixada a la pissarra la paràbola y = x2 i 100 rectes paral·leles a la recta y = x, de manera que cadascuna d’elles talla la paràbola en dos punts.
Quant val la suma dels valors de les abscisses x de tots aquests punts? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 534 › ›
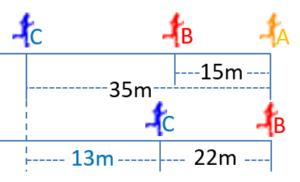
| L’Anna, en Bernat i en Carles corren una cursa. Surten junts i cadascú manté una velocitat constant. Quan l’Anna arriba al final, a en Bernat li falten 15 m per a acabar, i a en Carles, 35 m.
Quan en Bernat acaba, a en Carles li queden 22 m.
Quina és la longitud de la cursa? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 530 › ›
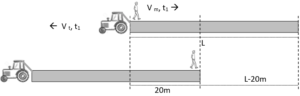
| En Marc va veure un tractor que arrossegava, a velocitat constant, un tub. Per tal de deduir quina era la longitud del tub, en Marc es va posar a caminar, també a velocitat constant, pel costat del tub. Primer va caminar en sentit contrari al del tractor i va haver de fer 20 passes per a anar d’una punta a l’altra. Després va caminar al costat del tub però en el mateix sentit que el tractor i va haver de fer 140 passes per a anar d’una punta a l’altra. Sabent que en Marc fa les passes d’1 m, quina és la longitud del tub? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 525 › ›
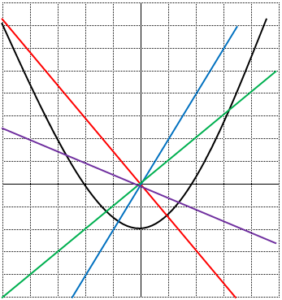
| Quatre línies rectes diferents passen per l’origen de coordenades. Les rectes intersequen la paràbola y = x2 − 2 en vuit punts.
Quin és el producte de les vuit coordenades x d’aquests punts? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 518 › ›
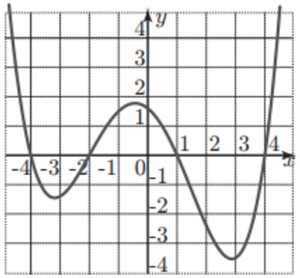
La figura mostra el gràfic d’una funció f : [−5; 5] → R.
Quantes solucions diferents té l’equació f(f(x)) = 0 ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 514 › ›
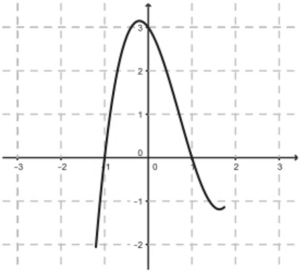
La figura mostra un tros de la gràfica de la funció f(x) = ax3 + bx2 + cx + d
Quin és el valor de b? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 505 › ›
| f(x) és una funció de nombres reals que compleix f(x + y) = f(x) · f(y) i f(1) = 2. Quin és el valor de l’expressió següent -> |
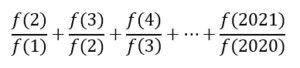 |
› › Clica per a veure el vídeo d’ACTIVITAT 503 › ›
| Un conill i un eriçó van participar en una cursa per una pista circular de 550 m de llargada, on coincideixen la sortida i l’arribada. La velocitat del conill era de 10 m/s i la de l’eriçó d’1 m/s. Van començar simultàniament. Però l’eriçó, amb ganes d’enganyar, va començar en la direcció contrària a la que corria el conill. Quan es van trobar, l’eriçó va girar cua immediatament i va córrer darrere del conill. Quant de temps després del conill va arribar l’eriçó a la meta? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 502 › ›
| Un meló pesa 7/5 kg més que les 5/7 parts del meló. Quant pesa el meló? |
 |
› › Clica per a veure el vídeo d’ACTIVTAT 500 › ›
| La funció f compleix f(x + y) = f(x) · f(y) per a tots els enters x i y.
Si f(1) = 1/2 , quin és el valor de f(0) + f(1) + f(2) + f(3)? |
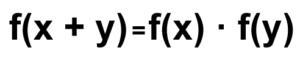 |
› › Clica per a veure el vídeo d’ACTIVITAT 495 › ›
Una funció definida en el conjunt de nombres reals positius compleix les dues condicions següents:
- y·f(x·y) = f(x) per a tot x, y enters i positius.
- f(32) = 63
Quant val f(24) ? |
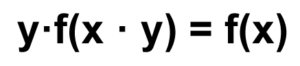 |
› › Clica per a veure el vídeo d’ACTIVITAT 494 › ›
| La paràbola de la figura té l’equació y = ax2 + bx + c.
Quina de les equacions següents podria ser l’equació de la recta de la figura? |
 |
| A) y = ax + b |
B) y = bx + c |
C) y = cx + a |
D) y = ax + c |
E) y = cx + b |
› › Clica per a veure el vídeo d’ACTIVITAT 487 › ›
| Una llebre i una tortuga competeixen en una cursa de 5 km al llarg d’una línia recta. La llebre és cinc vegades més ràpida que la tortuga. Per error, la llebre ha començat la cursa en direcció perpendicular a la línia fixada. Al cap d’una estona s’ha adonat del seu error, ha corregit la seva direcció i s’ha dirigit en línia recta cap al punt d’arribada. Ha arribat al mateix temps que la tortuga. Quina és la distància entre el punt on la llebre ha girat i el punt d’arribada? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 479 › ›
|
|