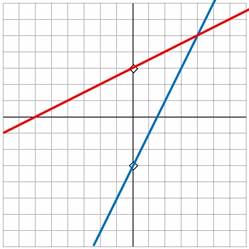
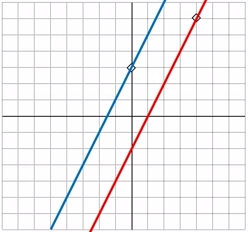
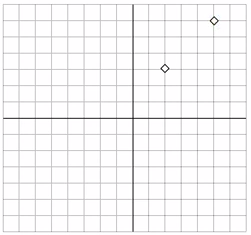
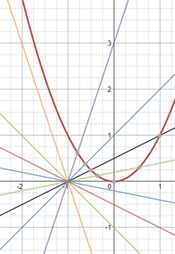
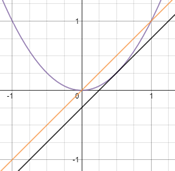
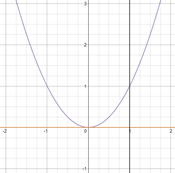
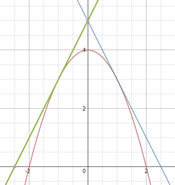
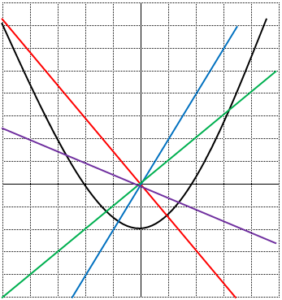
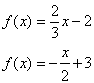| Quatre línies rectes diferents passen per l’origen de coordenades. Les rectes intersequen la paràbola y = x2 − 2 en vuit punts.
Quin és el producte de les vuit coordenades x d’aquests punts? |
 |
|
|||||||||||||||||||||||||||||||||||||||||||
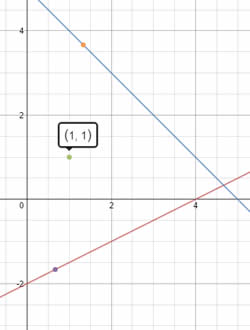
La funció afí (funció de 1r grau), propietats gràfiques – Aplicació Geogebra En aquesta aplicació pots modificar el pendent de la recta, què és m, i l’ordenada a l’origen, que és n i observar com varia la recta
|
|||||||||||||||||||||||||||||||||||||||||||
|
Copyright © 2025 PRoBLeMeS - email:correu@prblms.net Powered by WordPress & Atahualpa |
|||||||||||||||||||||||||||||||||||||||||||