| Una casa de 200 m2 es troba en una parcela, la distància a esquerra i dreta entre la tanca i la casa ha de ser de 3m i la distància a dalt i abaix ha de ser de 10 m. Quina és l’àrea mínima de la parcela, i la seva amplada |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 465 › ›
| Es vol construir una porteria de futbol amb un llistó de 16 metres de longitud. Quines són les mides que fan l’àrea més gran. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 459 › ›
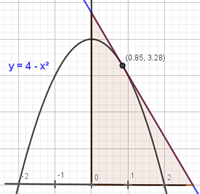
| En quin punt de la paràbola y = 4 – x2 la tangent forma amb els eixos de coordenades un triangle d’area mínima? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 440 › ›
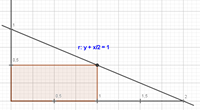
| De entre tots els rectangles situats en el primer quadrant que tenen dos dels seus costats sobre els eixos de coordenades i un vèrtex sobre la recta y + x/2 = 1, troba el que té la superfíciemes gran. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 439 › ›
| Una finestra té una superfície de 1 m2. Si el cost de l’amplada de la finestra és de 12,5 €/m i el cost de l’altura de la finestra és de 8 €/m. Troba les mides que aconsegueixen el preu més baix. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 438 › ›
La funció de 2n grau – Aplicació de Geogebra
Amb aquesta aplicació es pot estudiar el comportament de la funció de 2n grau.
Es pot veure com evoluciona la seva forma, eix de simetria; les arrels, el punt de tall amb l’eix d’ordenades, vèrtex, i eventualment el màxim / mínim; tot depenent dels coeficients.
› › Clica per a veure el vídeo d’ACTIVITAT 233 › ›
La funció afí (funció de 1r grau), propietats gràfiques – Aplicació Geogebra
En aquesta aplicació pots modificar el pendent de la recta, què és m, i l’ordenada a l’origen, que és n i observar com varia la recta
› › Clica per a veure el vídeo d’ACTIVITAT 232 › ›
l’El·lipse – Aplicació Geogebra
Els focus de l’el·lipse són dos punts F1 i F2 situats a l’eix major de l’el·lipse i equidistants del punt central. La suma de les distàncies des de qualsevol punt A de l’el·lipse als focus és constant i igual a l’eix major (R1 + R2 = Eix Major).
L’excentricitat d’una el·lipse, és el quocient de la distància entre els dos focus i la longitud de l’eix major. Per a una el·lipse l’excentricitat està entre 0 i 1.
Quan l’excentricitat és 0, els focus coincideixen amb el punt central i la figura és un cercle.
› › Clica per a veure el vídeo d’ACTIVITAT 231 › ›
Simetria Central – Aplicació Geogebra
Els polígons de la figura presenten simetria axial. Podeu modificar el polígon ABCD i tambe el centre de simetria H, i comprovareu que l’altre polígon és el reflex del primer respecte la recta R
› › Clica per a veure el vídeo d’ACTIVITAT 230 › ›
Simetria Axial – Aplicació Geogebra
Els polígons de la figura presenten simetria axial. Podeu modificar el polígon ABCD i també la posició relativa de la recta, i comprovareu que l’altre polígon és el reflex del primer respecte la recta HH’
› › Clica per a veure el vídeo d’ACTIVITAT 229 › ›
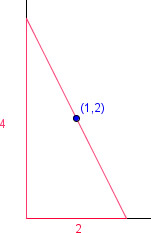
| De totes les rectes que passen pel el punt (1,2), troba la que determina amb els eixos de coordenades, en el primer quadrant, un triangle d’àrea mínima.
Aquest és un problema d’optimització que en aquest cas resolem amb una aplicació de Geogebra
També es pot resoldre buscant l’area del triangle en funció de la base, derivant l’expressió i igualant a zero per a buscar el valor de la base.
sigui x la base;
Area(x) = x2/(x-1) -> Area'(x) = (x² – 2x) / (x-1)² = 0 -> x² – 2x = 0 -> x = 2 -> Area (2)= 4 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 228 › ›
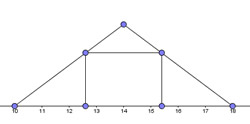
| Trobar les dimensions d’un rectangle inscrit dins un triangle isòsceles de base 8 cm i altura 3 cm.
En aquest cas el problema es resol amb una aplicació feta amb Geogebra |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 227 › ›
Geometria – Propietats de la Paràbola
Una de les seves propietats la fan molt interessant per a algunes conegudes aplicacions, com són les antenes parabòliques, els rajos electromagnètics que arriben a les antenes, surten desviats amb el mateix angle d’incidència quan arriben a la paràbola, i aquestos rajos van a parar al focus on es concentren, amplificant així el senyal electromagnètic. Els fars dels cotxes s’aprofiten de la mateixa situació, però a l’inrevés; la bombeta s’instal·la al focus d’un reflector en forma de paràbola, de manera que els rajos de llum surten paral·lels entre si i cap endavant. › › Clica per a veure el vídeo d’ACTIVITAT 226 › ›
Geometria – Homotècies en el pla
La homotècia és una transformació geomètrica que manté la forma de la figura, de manera que els costats de la homotècia són proporcionals als de la figura original.
Llisca el cursor (des de valor 0 a 5) per tal d’obtenir una homotècia de raó determinada (els costats tenen aquesta proporció).
› › Clica per a veure el vídeo d’ACTIVITAT 225 › ›
Una hipèrbola pot ser definida com el lloc geomètric dels punts on el valor absolut de la diferència de les distàncies als dos focus és una constant igual a 2 cops la distància entre els seus dos vèrtexs.
Similar a una paràbola, una hipèrbola és una corba oberta, el que significa que continua indefinidament fins a l’infinit. Consta de dues corbes desconnectades anomenats els seus braços. Els punts en les dues branques que estan més a prop entre si es diuen vèrtexs, i el segment de línia que els connecta es diu eix major. El punt mitjà de l’eix major es coneix com a centre de la hipèrbola. A la mateixa recta de l’eix major hi ha els dos punts focals (focus) de la hipèrbola. La línia a través d’aquests cinc punts és un dels dos eixos principals de la hipèrbola, sent l’altra la bisectriu perpendicular de l’eix major. La hipèrbola té simetria de mirall al voltant dels seus eixos principals, i també és simètrica sota un gir de 180 ° al voltant del seu centre. A grans distàncies del centre, la hipèrbola s’aproxima a dues rectes, les asímptotes, que es creuen en el centre de la hipèrbola.
En alguns problemes apareix una versió simplificada de la hipèrbola, Y = 1/X, què és una hipèrbola equilàtera, en aquest cas els braços estan als quadrants I i III, els eixos de la hipèrbola són les bisectrius dels quadrants (45º), i les asímtotes, són els eixos de cordenades).
› › Clica per a veure el vídeo d’ACTIVITAT 224 › ›
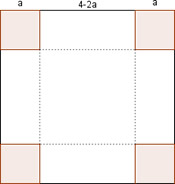
| Disposem d’una cartolina quadrada de 4 cm de costat amb la qual volem construir una capsa de base quadrada segons la imatge. Quin ha de ser el tall ‘a’ per tal que el volum sigui el màxim possible?
Aquest problema es pot resoldre derivant l’expressió del volum en funció de ‘a’ i igualant a zero, però en aquest cas es fa amb una aplicació de geogebra.
V(a)=(4 – 2a)·(4 – 2a)·a = 4a3 – 16a2 + 16a –> V'(a)= 12a2 – 16a + 16 = 0
a= 2/3 cm –> Vmax=4,74 cm3
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 223 › ›
Propietats de la funció exponencial i logarítmica
Funció exponencial es refereix a qualsevol funció del tipus kax, on ‘a’ és qualsevol nombre real positiu:
•La funció només està definida per a valors positius de la base de la potència.
•La funció de base ‘a’ i la seva inversa (1/a) presenten simetria axial vertical.
•Domini : R
•Recorregut : R+
•L’asímptota és l’eix d’abcisses
Té com a funció inversa la Funció Logaritme
•La funció només està definida per a valors positius de la base del logaritme.
•La funció de base ‘a’ i la seva inversa (1/a) presenten simetria axial horitzontal.
•Domini : R+
•Recorregut : R
•L’asímptota és l’eix d’ordenades
El cas particular on la base és el número ‘e’ , també es diu funció exponencial de base ‘e’, és una de les funcions més importants de les matemàtiques. S’escriu com exp(x) o ex, on e val aproximadament 2.71828183 i és la base dels logaritme natural o neperià. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 222 › ›
|
|
















