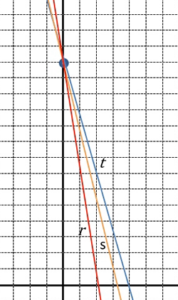
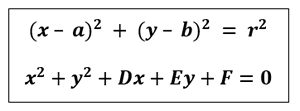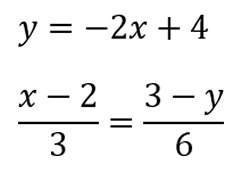| Donades les rectes r: 3x + my – 7 = 0, s: 4x + y – 14 = 0, t: 7x + 2y – 28 = 0 determina m perquè les tres siguin rajos d’un mateix feix de rectes. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 613 › ›
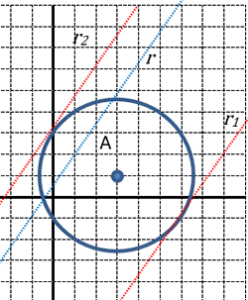
| Donada l’equació de la circumferència x2 + y2 – 6x – 2y – 4 = 0, busca les equacions tangents, paral·leles a la recta r: 4x – 3y + 2 = 0? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 612 › ›
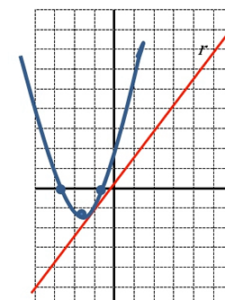
| Busca el valor de a perquè la recta r: 4x – 3y + a = 0 sigui tangent a la paràbola 3y = 3x2 + 10x + 4 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 611 › ›
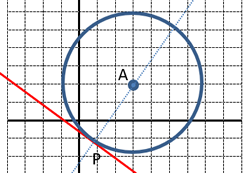
| Busca l’equació de la circumferència que té el centre a A(3,2) i és tangent a la recta r1 : 3x + 4y + 2 = 0 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 610 › ›
Busca l’equació de la circumferència en els casos següents:
a) Té el centre a (1,4) i passa per A(-6,-1)
b) Té per diàmetre els punts A(2,3) i B(-5,2)
c) Passa pels punts A(1,0),B(3,-2)C(1,-4) |
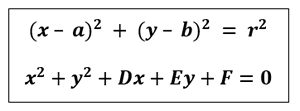 |
› › Clica per a veure el vídeo d’ACTIVITAT 609 › ›
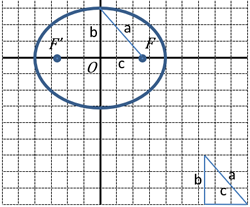
| Busca els eixos, distancia focal i excentricitat de l’el·lipse que té com a equació 9×2 + 16y2 = 144. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 608 › ›
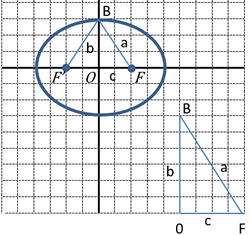
| Busca l’equació de l’el·lipse que té els focus F’(-2,0) i F(2,0) i que la suma de les distàncies a qualsevol n punt és 7. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 607 › ›
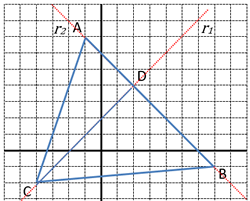
| Els punts A(-1,7), B(7,-1) i C(-4,-2), formen un triangle, troba la seva àrea |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 606 › ›
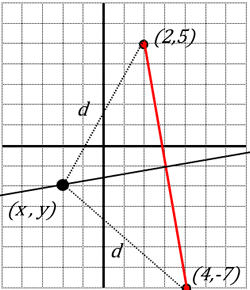
| Troba la recta mediatriu del segment d’extrems A(2,5) i B(4,-7) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 605 › ›
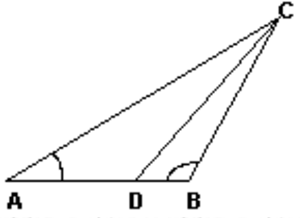
| La figura inferior mostra un triangle ABC en què l’angle A = 30º, l’angle B = 120º i la recta CD és la bisectriu de l’angle ACB.
Quin és el valor de la raó BC/CD ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 602 › ›
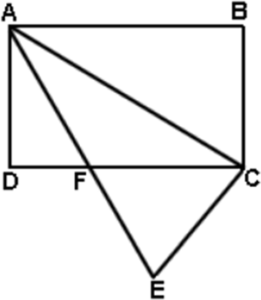
En la figura, ABCD és un rectangle amb AB = 16 cm i BC = 12 cm. ACE és un triangle rectangle amb AC ⊥ CE i CE = 15 cm.
Si F és el punt d’intersecció dels segments AE i CD, llavors quant val l’àrea de AFC? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 601 › ›
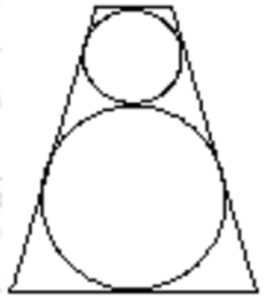
A l’interior d’un trapezi isòsceles de bases 9 cm i 1 cm, s’han inscrit dos cercles tangents, de manera que el radi del gros és el triple del radi del petit.
Quina mesura, expressada en centímetres, tenen els costats iguals del trapezi? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 598 › ›
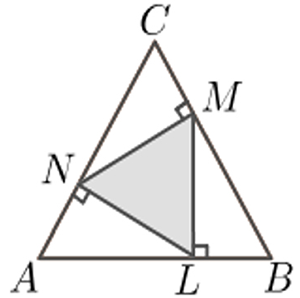
En els costats d’un triangle equilàter ABC, que té l’àrea igual a 36 cm2, hi ha tres punts N, M i L, amb la propietat que LM és perpendicular a AB, MN és perpendicular a BC i NL és perpendicular a CA.
Quina és l’àrea del triangle LMN? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 597 › ›
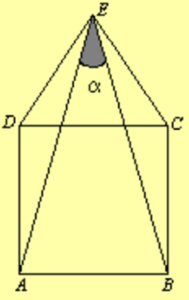
| A la figura, ABCD és un quadrat i CED és un triangle equilàter.
L’angle α és igual a… |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 596 › ›
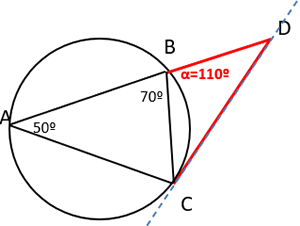
| Un triangle ABC amb A = 50º , B = 70º , està inscrit en un cercle.
La tangent a aquest cercle en el punt C talla la prolongació del costat AB al punt D.
Quant mesuren els angles del triangle BCD? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 592 › ›
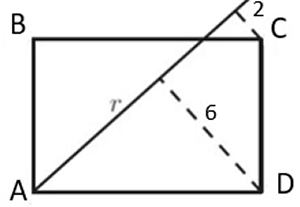
La recta r passa pel vèrtex A d’un rectangle ABCD. La distància des del punt C a la recta r és 2, i la distància des del punt D a la recta r és 6.
Si la longitud del costat AD és el doble que la del costat AB, quina és la longitud de AD? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 585 › ›
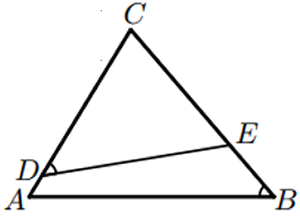
Les longituds dels costats d’un triangle △ABC són AB = 10, BC = 9 i CA = 8. El punt D és un punt del costat CA i compleix CD = 7 i el punt E és un punt del costat BC, de manera que els angles ABC i CDE són iguals.
Quin és el perímetre del triangle △CDE ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 584 › ›
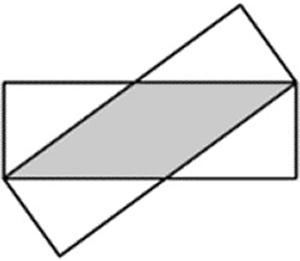
| Posem, un a sobre de l’altre, dos rectangles idèntics amb costats de 3 cm i 9 cm de longitud, com es mostra en la figura.
Quina és l’àrea de la intersecció dels dos rectangles? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 583 › ›
|
|