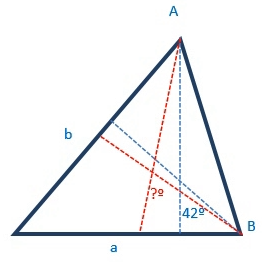
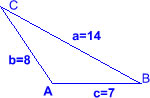
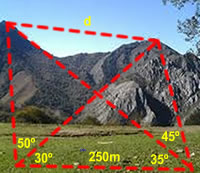
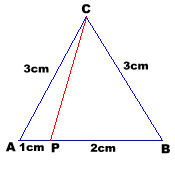
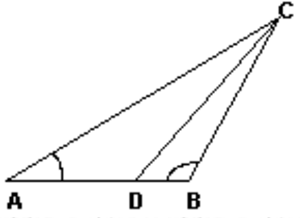
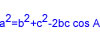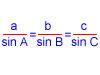Angles i raons trigonomètriques

ACTIVITAT 602

La figura inferior mostra un triangle ABC en què l’angle A = 30º, l’angle B = 120º i la recta CD és la bisectriu de l’angle ACB.

Quin és el valor de la raó BC/CD ?

› › Clica per a veure el vídeo d’ACTIVITAT 602 › ›

En la figura, ABCD és un rectangle amb AB = 16 cm i BC = 12 cm. ACE és un triangle rectangle amb AC ⊥ CE i CE = 15 cm.
Si F és el punt d’intersecció dels segments AE i CD, llavors quant val l’àrea de AFC?

› › Clica per a veure el vídeo d’ACTIVITAT 601 › ›

ACTIVITAT 596

A la figura, ABCD és un quadrat i CED és un triangle equilàter.

L’angle α és igual a…

› › Clica per a veure el vídeo d’ACTIVITAT 596 › ›

ACTIVITAT 587

Quin angle és més gran?

› › Clica per a veure el vídeo d’ACTIVITAT 587 › ›

ACTIVITAT 548

Quant mesura l’angle α de l’estrella regular de cinc puntes de la figura?

› › Clica per a veure el vídeo d’ACTIVITAT 548 › ›

ACTIVITAT 526

L’angle que formen les altures corresponents als costats a i b d’un triangle acutangle △ABC mesura 42◦ .

Quant mesura l’angle que formen les bisectrius corresponents als vèrtexs A i B?

› › Clica per a veure el vídeo d’ACTIVITAT 526 › ›

ACTIVITAT 491

Dos rectangles estan situats, com indica la figura, amb angles de 40º i 30º respecte a una recta.

Quina és la mesura de l’angle θ?

› › Clica per a veure el vídeo d’ACTIVITAT 491 › ›

ACTIVITAT 351

[IBO] Troba els costats i angles del triangle de la figura

› › Clica per a veure el vídeo d’ACTIVITAT 351 › ›

ACTIVITAT 293

[PAAU 2000] Els costats d’un triangle són de longituds 8 cm, 11 cm i 13 cm. Calculeu el sinus de l’angle més petit.

› › Clica per a veure el vídeo d’ACTIVITAT 293 › ›

ACTIVITAT 286

Troba els angles del triangle de la figura

› › Clica per a veure el vídeo d’ACTIVITAT 286 › ›

ACTIVITAT 277

Troba la distància entre els dos cims amb l’ajut de les triangulacions que s’indiquen a l’esquema

› › Clica per a veure el vídeo d’ACTIVITAT 277 › ›

ACTIVITAT 276

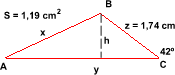
Demostració de la fórmula del cosinus de la suma de dos angles aguts
cos(A+B)= cosA·cosB – sinA·sinB

› › Clica per a veure el vídeo d’ACTIVITAT 276 › ›

ACTIVITAT 275

Demostració de la fórmula del sinus de la suma de dos angles aguts
sin(A+B)= sinA·cosB + sinB·cosA

› › Clica per a veure el vídeo d’ACTIVITAT 275 › ›

ACTIVITAT 274

Demostració del Teorema del Cosinus

› › Clica per a veure el vídeo d’ACTIVITAT 274 › ›

ACTIVITAT 273

Demostració del Teorema del Sinus

› › Clica per a veure el vídeo d’ACTIVITAT 273 › ›

ACTIVITAT 264

[PAAU 2001] Siguin A, B i C els tres vèrtex d’un triangle equilàter de costat 3 cm i P el punt del costat AB qu és a 1 cm del vèrtex A. Quina és la longitud del segment CP?

› › Clica per a veure el vídeo d’ACTIVITAT 264 › ›

ACTIVITAT 260

Troba la superfície d’un hexàgon regular, sabent que l’apotema val 10 cm (De pas troba l’angle central i interior de l’hexàgon regular)

› › Clica per a veure el vídeo d’ACTIVITAT 260 › ›

ACTIVITAT 252

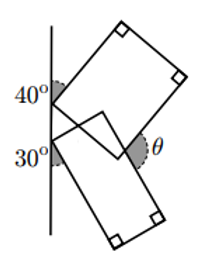
Raonament sobre la relació d’angles complementaris, suplementaris, oposats, i amb diferència de 90º i 180º

› › Clica per a veure el vídeo d’ACTIVITAT 252 › ›

ACTIVITAT 221

Veiem el cim d’una torre sota un angle de 16,7º, avancem 10 m i aleshores el veiem sota un angle de 31º. Es demana la distància des del punt inicial a la base de la torre i la seva alçada

› › Clica per a veure el vídeo d’ACTIVITAT 221 › ›

ACTIVITAT 200

[PAAU 2001]Els tres costats d’un triangle mesuren 3 cm, 4 cm i 5 cm . Calculeu els seus angles i la seva àrea.

› › Clica per a veure el vídeo d’ACTIVITAT 200 › ›

PRoBLeMeS