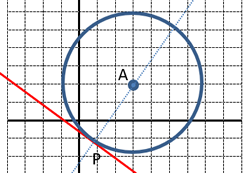
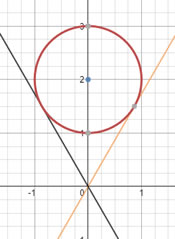
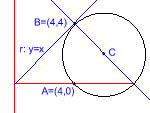
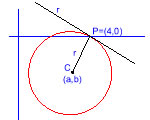
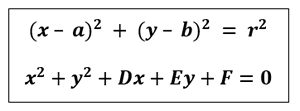| Donada l’equació de la circumferència x2 + y2 – 6x – 2y – 4 = 0, busca les equacions tangents, paral·leles a la recta r: 4x – 3y + 2 = 0? | 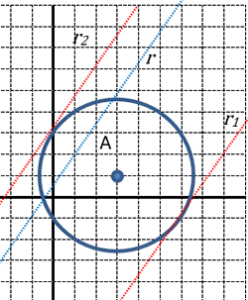 |
|
|||||||||||
|
|||||||||||
|
Copyright © 2025 PRoBLeMeS - email:correu@prblms.net Powered by WordPress & Atahualpa |
|||||||||||