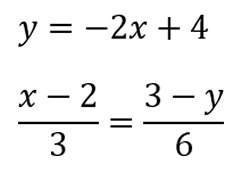| Donades les rectes r: 3x + my – 7 = 0, s: 4x + y – 14 = 0, t: 7x + 2y – 28 = 0 determina m perquè les tres siguin rajos d’un mateix feix de rectes. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 613 › ›
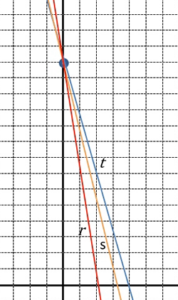
| Donada l’equació de la circumferència x2 + y2 – 6x – 2y – 4 = 0, busca les equacions tangents, paral·leles a la recta r: 4x – 3y + 2 = 0? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 612 › ›
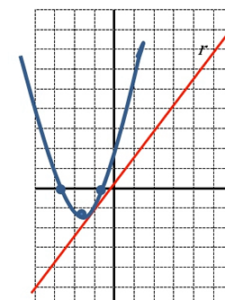
| Busca el valor de a perquè la recta r: 4x – 3y + a = 0 sigui tangent a la paràbola 3y = 3x2 + 10x + 4 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 611 › ›
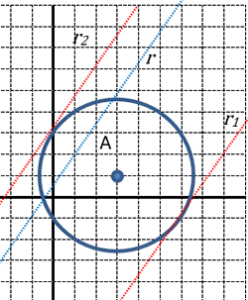
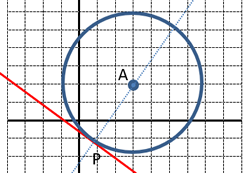
| Busca l’equació de la circumferència que té el centre a A(3,2) i és tangent a la recta r1 : 3x + 4y + 2 = 0 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 610 › ›
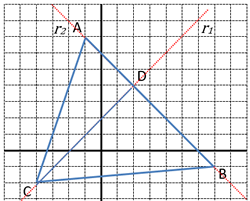
| Els punts A(-1,7), B(7,-1) i C(-4,-2), formen un triangle, troba la seva àrea |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 606 › ›
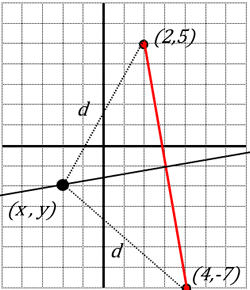
| Troba la recta mediatriu del segment d’extrems A(2,5) i B(4,-7) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 605 › ›
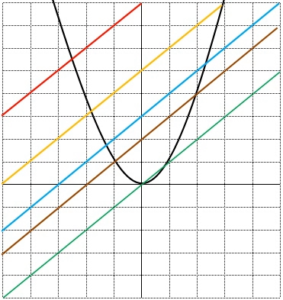
| En acabar la classe de matemàtiques ha quedat dibuixada a la pissarra la paràbola y = x2 i 100 rectes paral·leles a la recta y = x, de manera que cadascuna d’elles talla la paràbola en dos punts.
Quant val la suma dels valors de les abscisses x de tots aquests punts? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 534 › ›
| Troba l’equació explicita del a recta que passa pels punts A(2,3) i B(3,5). |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 461 › ›
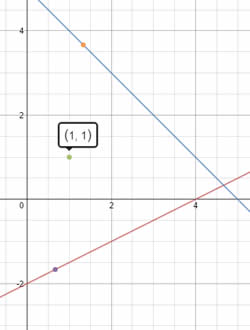
| [IBO] El gràfic mostra les rectes x + y = 5 i x – 2y – 4 = 0, i també el punt P (1,1). És dibuixa una recta que passant per P talli les dues rectes anteriors pels punts R i Q respectivament, de manera que P sigui el punt mig del segment RQ. Es demana trobar les coordenades dels punts R i Q |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 371 › ›
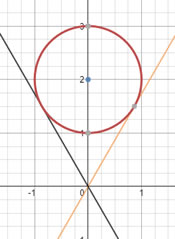
| [IBO] Donat el cercle x² + (y – 2)² = 1, trobeu els possibles pendents de la recta y=kx, tal que sigui tangent al cercle. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 362 › ›
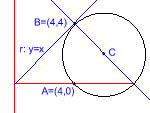
[PAAU 2001] La circumferència C passa pel punt A=(4,0) i és tangent a la recta y=x en el punt B=(4,4).
a) Determineu l’equació de la recta que passa per B i el centre de la circumferència C.
b) Trobeu el centre de C i calculeu el seu radi. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 298 › ›
| Comprova si els punts A(-3,-2), B(0,1), C(4,5) estan o no alineats |
|
› › Clica per a veure el vídeo d’ACTIVITAT 211 › ›
| Donada la recta y= 3x – 2, escriu la seva expressió en forma vectorial. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 180 › ›
| Donats els punts A(-2,-1) i B (1,5) troba l’equació de la recta que passa per aquests punts en forma: vectorial, paramètrica, continua, punt pendent, i explícita |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 179 › ›
|
|