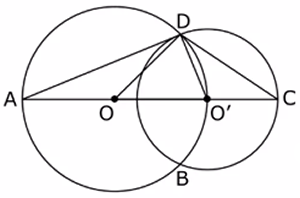
| DAC =20º, O i O’ són els centres de les circumferències.
Quant val ACD i ODO’ i ADC? ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 581 › ›
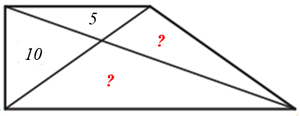
El quadrilàter de la imatge és un trapezi rectangle. Els nombres mostren les àrees de dos dels triangles interiors.
Quina és l’àrea del trapezi? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 579 › ›
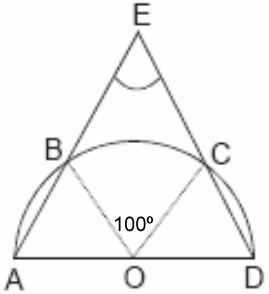
| A la semicircumferència de centre O de la figura, ∠ BOC fa 100º. △ AED és isòsceles.
Troba tots els angles |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 576 › ›
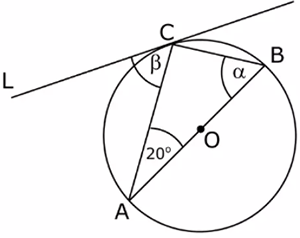
La recta L és tangent a la circumferència al punt on hi el vèrtex C del triangle,
quant val α i β |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 574 › ›
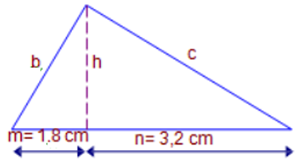
Tenim un triangle rectangle, de manera que l’alçada relativa a la hipotenusa determina sobre aquesta dos segments de longituds 1,8 cm i 3,2 cm.
Troba: |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 566 › ›
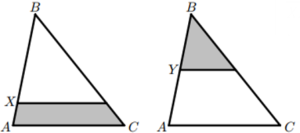
En el triangle △ABC dibuixem una línia paral·lela a la base AC que passa pel punt X i una altra pel punt Y. Les àrees de les regions ombrejades són iguals. La raó BX:XA és 4:1.
Quina és la raó BY:YA? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 559 › ›
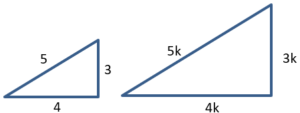
Els tres costats d’un triangle són proporcionals als d’un altre triangle de valors 3, 4, 5.
Troba els costats d’aquest triangle sabent que la seva àrea és de 54 m2. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 549 › ›
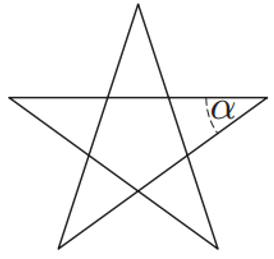
| Quant mesura l’angle α de l’estrella regular de cinc puntes de la figura? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 548 › ›
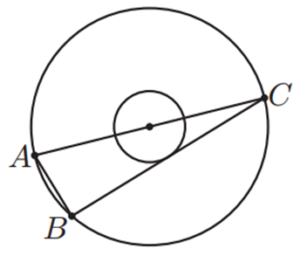
| Els radis de dues circumferències concèntriques estan en proporció 1:3. El segment AC és el diàmetre de la circumferència gran, BC és una corda de la circumferència gran que és tangent a la circumferència petita, i la longitud de AB és 12.
Quin és el radi de la circumferència gran? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 547 › ›
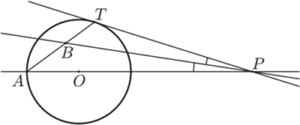
En la figura, la recta PT és tangent a la circumferència de centre O, i PB és la bisectriu de l’angle TPA.
Quant fa l’angle ABP? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 543 › ›
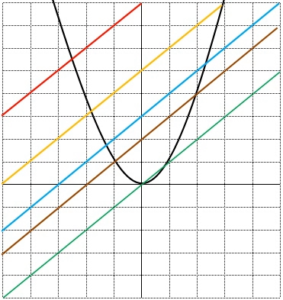
| En acabar la classe de matemàtiques ha quedat dibuixada a la pissarra la paràbola y = x2 i 100 rectes paral·leles a la recta y = x, de manera que cadascuna d’elles talla la paràbola en dos punts.
Quant val la suma dels valors de les abscisses x de tots aquests punts? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 534 › ›
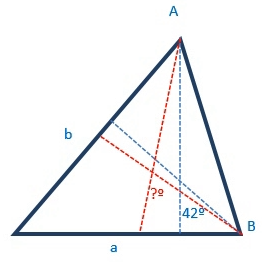
| L’angle que formen les altures corresponents als costats a i b d’un triangle acutangle △ABC mesura 42◦ .
Quant mesura l’angle que formen les bisectrius corresponents als vèrtexs A i B? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 526 › ›
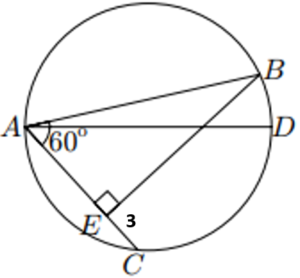
| En un cercle de diàmetre AD hem dibuixat dues cordes, AB i AC, de manera que BAC = 60º. Tracem BE perpendicular a AC i resulta que el segment EC fa 3 cm.
Quina és la longitud del segment BD (no dibuixat a la figura)? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 520 › ›
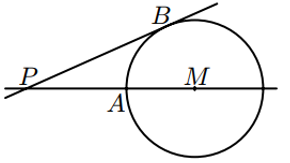
| A i B són dos punts d’una circumferència de centre M. El punt P és a la recta AM i la recta PB és tangent a la circumferència en el punt B. Les distàncies PA i MB són nombres enters i PB = PA + 6.
Quants valors diferents pot tenir el radi MB? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 519 › ›
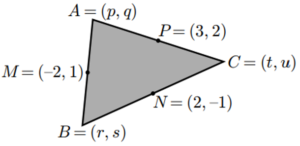
| Els tres vèrtexs d’un triangle són A = (p, q), B = (r, s) i C = (t, u), com es mostra a la figura. Els punts mitjans dels costats del triangle són els punts M = (−2, 1), N = (2, −1) i P = (3, 2).
Quin és el valor de p + q + r + s + t + u ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 512 › ›
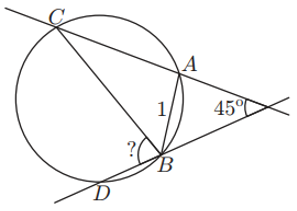
| Les línies rectes que contenen les cordes AC i BD d’una circumferència de radi 1 formen un angle de 45◦ i la corda AB té longitud 1.
Quant fa l’angle CBD?
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 508 › ›
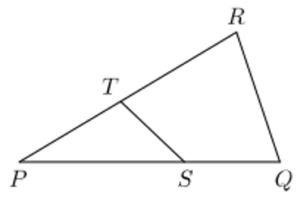
| En el triangle PQR, el punt S divideix el costat PQ, de tal manera que PS/SQ = 2. El punt T és un punt del costat PR que fa que l’àrea del triangle PST sigui la meitat de l’àrea del triangle PQR. Quin és el valor de PT/TR ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 501 › ›
|
|
