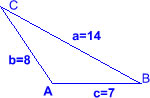
La figura mostra un semicercle amb centre en el punt O. En coneixem dos angles, de 32º i 67º.
Quina mida té l’angle α? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 497 › ›
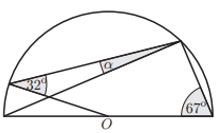
| El trapezi isòsceles de la figura té els costats paral·lels de longitud 3 i 7.
Quin percentatge de l’àrea del trapezi és verda? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 496 › ›
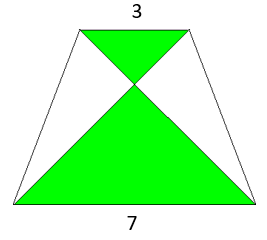
| Dos rectangles estan situats, com indica la figura, amb angles de 40º i 30º respecte a una recta.
Quina és la mesura de l’angle θ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 491 › ›
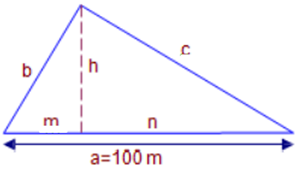
Tenim un triangle rectangle, com el de la figura on es coneix la hipotenusa a=100 m i l’àrea A=2400 m2. Troba:
a) La longitud de l’alçada corresponent a la hipotenusa.
b) la longitud de n
c) la longitud del catet b. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 485 › ›
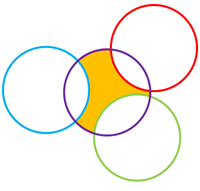
| Quatre cercles de radi 1 es tallen com en la figura. Quin és el perímetre de la zona acolorida? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 475 › ›
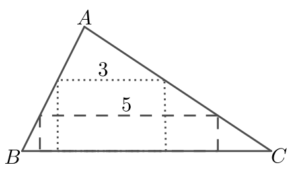
| Dos rectangles de costats 3 x 2, i 5 x 1, estan inscrits en el triangle ABC. Quina és l’altura del triangle? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 473 › ›
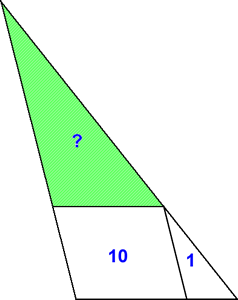
| En un triangle hi hem inscrit un paral·lelogram d’àrea 10, com es veu a la figura. El triangle petit a la seva dreta té àrea 1.
Quant mesura l’àrea del triangle verd? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 472 › ›
| Troba l’equació explicita del a recta que passa pels punts A(2,3) i B(3,5). |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 461 › ›
Representa la paràbola (Y – 3)2 = – 4(X + 2), trobant els elements d’interès de la figura i la seva expressió general
› › Clica per a veure el vídeo d’ACTIVITAT 399 › ›
| [CB 4t ESO] Resolució de les activitats de Matemàtiques de les Competències Bàsiques de 4t d’ESO del curs 2017-18 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 390 › ›
| [CB 4t ESO] Resolució de les activitats de Matemàtiques de les Competències Bàsiques de 4t d’ESO del curs 2018-19 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 389 › ›
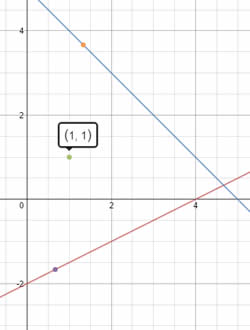
| [IBO] El gràfic mostra les rectes x + y = 5 i x – 2y – 4 = 0, i també el punt P (1,1). És dibuixa una recta que passant per P talli les dues rectes anteriors pels punts R i Q respectivament, de manera que P sigui el punt mig del segment RQ. Es demana trobar les coordenades dels punts R i Q |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 371 › ›
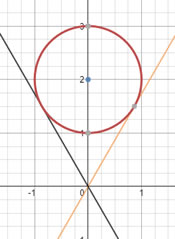
| [IBO] Donat el cercle x² + (y – 2)² = 1, trobeu els possibles pendents de la recta y=kx, tal que sigui tangent al cercle. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 362 › ›
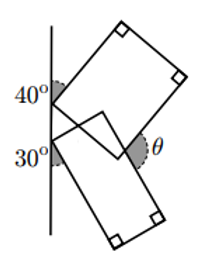
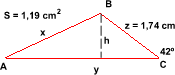
| [IBO] Troba els costats i angles del triangle de la figura |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 351 › ›
| [IBO] Troba l’àrea del segment circular limitada per la corda AB |
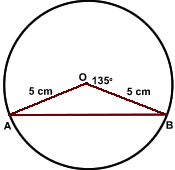 |
› › Clica per a veure el vídeo d’ACTIVITAT 350 › ›
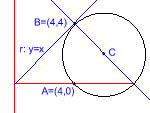
[PAAU 2001] La circumferència C passa pel punt A=(4,0) i és tangent a la recta y=x en el punt B=(4,4).
a) Determineu l’equació de la recta que passa per B i el centre de la circumferència C.
b) Trobeu el centre de C i calculeu el seu radi. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 298 › ›
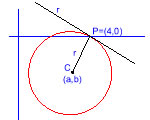
[PAAU 2000] Considereu la circumferència x² + y² – 6x + 4y + 8 =0
a) Calculeu-ne el centre i el radi
b) Comproveu que el punt P(4,0) està contingut a la circumferència i determineu l’equació de la recta tangent a aquest punt (la recta tangent en un punt d’una circumferència és la perpendicular al radi que passa per aquest punt). |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 295 › ›
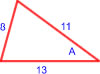
| [PAAU 2000] Els costats d’un triangle són de longituds 8 cm, 11 cm i 13 cm. Calculeu el sinus de l’angle més petit. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 293 › ›
| Troba la distància entre els dos cims amb l’ajut de les triangulacions que s’indiquen a l’esquema |
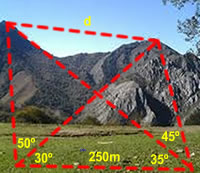 |
› › Clica per a veure el vídeo d’ACTIVITAT 277 › ›
|
|