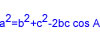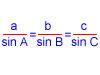Demostració de la fórmula del cosinus de la suma de dos angles aguts
cos(A+B)= cosA·cosB – sinA·sinB
› › Clica per a veure el vídeo d’ACTIVITAT 276 › ›
Demostració de la fórmula del sinus de la suma de dos angles aguts
sin(A+B)= sinA·cosB + sinB·cosA
› › Clica per a veure el vídeo d’ACTIVITAT 275 › ›
| [PAAU 2001] Siguin A, B i C els tres vèrtex d’un triangle equilàter de costat 3 cm i P el punt del costat AB qu és a 1 cm del vèrtex A. Quina és la longitud del segment CP? |
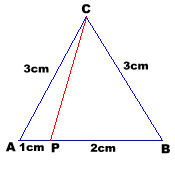 |
› › Clica per a veure el vídeo d’ACTIVITAT 264 › ›
| Troba la superfície d’un hexàgon regular, sabent que l’apotema val 10 cm (De pas troba l’angle central i interior de l’hexàgon regular) |
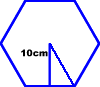 |
› › Clica per a veure el vídeo d’ACTIVITAT 260 › ›
| Aplicant el Teorema de Thales i les propietats dels triangles semblants, troba el valor dels segments: a, b, c, d |
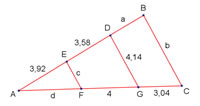 |
› › Clica per a veure el vídeo d’ACTIVITAT 258 › ›
Troba la hipotenusa del triangle que té per catets 3 i 4
Troba el catet del triangle que té per hipotenusa 4,5 i l’altre catet val 2 |
|
› › Clica per a veure el vídeo d’ACTIVITAT 256 › ›
| Troba el valor que ha de tenir la hipotenusa d’un triangle si sabem que un catet és el doble de gran que l’altre. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 255 › ›
Comprova si els triangles que tenen per costats:
a) 5, 12, 13
b) 3, 4, 6
c) 4, 9, 9
són o no triangles rectangles |
|
› › Clica per a veure el vídeo d’ACTIVITAT 254 › ›
Raonament sobre la relació d’angles complementaris, suplementaris, oposats, i amb diferència de 90º i 180º
› › Clica per a veure el vídeo d’ACTIVITAT 252 › ›
| Calcula el volum i superfície lateral de la tassa que veus fotografiada |
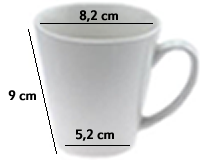 |
› › Clica per a veure el vídeo d’ACTIVITAT 234 › ›
La funció de 2n grau – Aplicació de Geogebra
Amb aquesta aplicació es pot estudiar el comportament de la funció de 2n grau.
Es pot veure com evoluciona la seva forma, eix de simetria; les arrels, el punt de tall amb l’eix d’ordenades, vèrtex, i eventualment el màxim / mínim; tot depenent dels coeficients.
› › Clica per a veure el vídeo d’ACTIVITAT 233 › ›
La funció afí (funció de 1r grau), propietats gràfiques – Aplicació Geogebra
En aquesta aplicació pots modificar el pendent de la recta, què és m, i l’ordenada a l’origen, que és n i observar com varia la recta
› › Clica per a veure el vídeo d’ACTIVITAT 232 › ›
l’El·lipse – Aplicació Geogebra
Els focus de l’el·lipse són dos punts F1 i F2 situats a l’eix major de l’el·lipse i equidistants del punt central. La suma de les distàncies des de qualsevol punt A de l’el·lipse als focus és constant i igual a l’eix major (R1 + R2 = Eix Major).
L’excentricitat d’una el·lipse, és el quocient de la distància entre els dos focus i la longitud de l’eix major. Per a una el·lipse l’excentricitat està entre 0 i 1.
Quan l’excentricitat és 0, els focus coincideixen amb el punt central i la figura és un cercle.
› › Clica per a veure el vídeo d’ACTIVITAT 231 › ›
Simetria Central – Aplicació Geogebra
Els polígons de la figura presenten simetria axial. Podeu modificar el polígon ABCD i tambe el centre de simetria H, i comprovareu que l’altre polígon és el reflex del primer respecte la recta R
› › Clica per a veure el vídeo d’ACTIVITAT 230 › ›
Simetria Axial – Aplicació Geogebra
Els polígons de la figura presenten simetria axial. Podeu modificar el polígon ABCD i també la posició relativa de la recta, i comprovareu que l’altre polígon és el reflex del primer respecte la recta HH’
› › Clica per a veure el vídeo d’ACTIVITAT 229 › ›
| De totes les rectes que passen pel el punt (1,2), troba la que determina amb els eixos de coordenades, en el primer quadrant, un triangle d’àrea mínima.
Aquest és un problema d’optimització que en aquest cas resolem amb una aplicació de Geogebra
També es pot resoldre buscant l’area del triangle en funció de la base, derivant l’expressió i igualant a zero per a buscar el valor de la base.
sigui x la base;
Area(x) = x2/(x-1) -> Area'(x) = (x² – 2x) / (x-1)² = 0 -> x² – 2x = 0 -> x = 2 -> Area (2)= 4 |
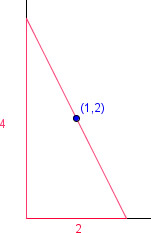 |
› › Clica per a veure el vídeo d’ACTIVITAT 228 › ›
Geometria – Homotècies en el pla
La homotècia és una transformació geomètrica que manté la forma de la figura, de manera que els costats de la homotècia són proporcionals als de la figura original.
Llisca el cursor (des de valor 0 a 5) per tal d’obtenir una homotècia de raó determinada (els costats tenen aquesta proporció).
› › Clica per a veure el vídeo d’ACTIVITAT 225 › ›
|
|