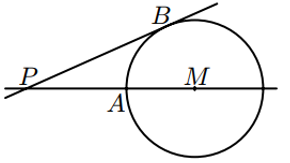
| A i B són dos punts d’una circumferència de centre M. El punt P és a la recta AM i la recta PB és tangent a la circumferència en el punt B. Les distàncies PA i MB són nombres enters i PB = PA + 6.
Quants valors diferents pot tenir el radi MB? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 519 › ›
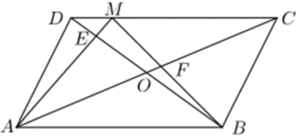
| La figura mostra un paral·lelogram ABCD d’àrea S. La intersecció de les diagonals del paral·lelogram és el punt O. El punt M es troba sobre el costat DC. La intersecció del segment AM amb la diagonal BD és el punt E i la intersecció del segment MB amb la diagonal AC és el punt F. La suma de les àrees dels triangles AED i BFC és S/3.
Quina és l’àrea del quadrilàter EOFM? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 516 › ›
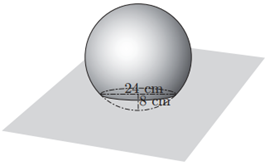
| Una pilota que estava flotant en un estany ha quedat enganxada quan aquest s’ha glaçat. En treure-la, ha quedat un clot en el gel de 24 cm de diàmetre i 8 cm de fondària.
Quin era el radi de la pilota? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 515 › ›
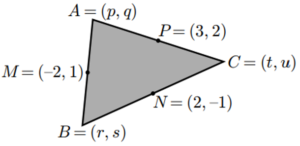
| Els tres vèrtexs d’un triangle són A = (p, q), B = (r, s) i C = (t, u), com es mostra a la figura. Els punts mitjans dels costats del triangle són els punts M = (−2, 1), N = (2, −1) i P = (3, 2).
Quin és el valor de p + q + r + s + t + u ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 512 › ›
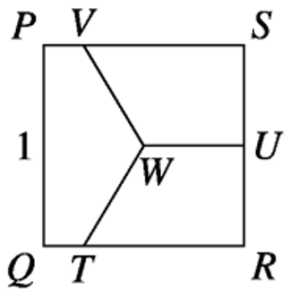
| El diagrama mostra el quadrat PQRS de costat 1. El punt mitjà de RS est marcat amb U i el centre del quadrat està marcat amb W. Els segments TW, UW i VW divideixen el quadrat en tres regions d’igual àrea.
Quina és la longitud de SV? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 511 › ›
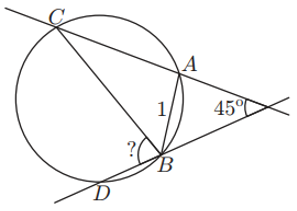
| Les línies rectes que contenen les cordes AC i BD d’una circumferència de radi 1 formen un angle de 45◦ i la corda AB té longitud 1.
Quant fa l’angle CBD?
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 508 › ›
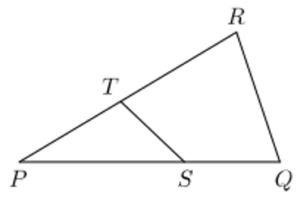
| En el triangle PQR, el punt S divideix el costat PQ, de tal manera que PS/SQ = 2. El punt T és un punt del costat PR que fa que l’àrea del triangle PST sigui la meitat de l’àrea del triangle PQR. Quin és el valor de PT/TR ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 501 › ›
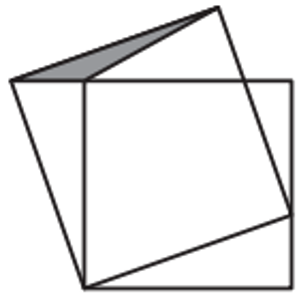
El quadrat petit de la figura té àrea 16 i el triangle gris té àrea 1.
Quant val l’àrea del quadrat gran? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 499 › ›
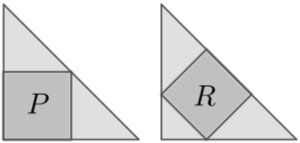
| Dos triangles isòsceles rectangles iguals tenen dos quadrats inscrits tal com es mostra en la figura. El quadrat P té àrea 45 unitats quadrades.
Trobeu l’àrea del quadrat R. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 498 › ›
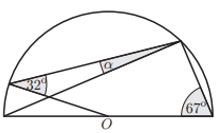
La figura mostra un semicercle amb centre en el punt O. En coneixem dos angles, de 32º i 67º.
Quina mida té l’angle α? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 497 › ›
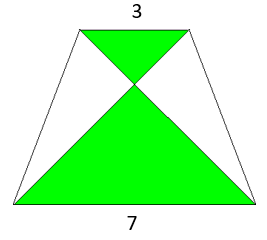
| El trapezi isòsceles de la figura té els costats paral·lels de longitud 3 i 7.
Quin percentatge de l’àrea del trapezi és verda? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 496 › ›
En l’estació espacial, un astronauta fa l’experiment següent: uneix dues esferes de mercuri en una sola esfera. Si cadascuna de les esferes menudes té una superfície de 2 mm2.
Quina és la superfície de la nova esfera? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 492 › ›
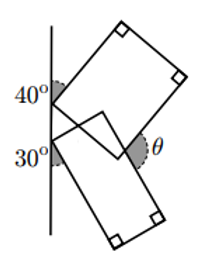
| Dos rectangles estan situats, com indica la figura, amb angles de 40º i 30º respecte a una recta.
Quina és la mesura de l’angle θ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 491 › ›
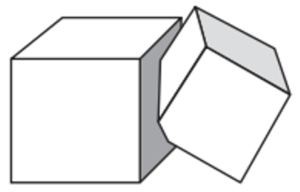
| Dos cubs de volums V i W s’intersequen. La part del cub de volum V que no és comuna als dos cubs és el 90 % del seu volum. La part del cub de volum W que no és comuna als dos cubs és el 85 % del seu volum.
Quina és la relació entre V i W? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 490 › ›
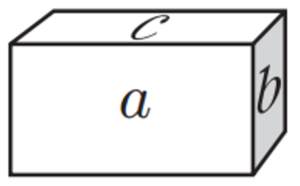
Les cares d’un maó ortoèdric tenen les àrees a, b i c com es mostra a la figura.
Quin és el volum del maó? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 489 › ›
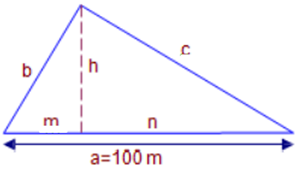
Tenim un triangle rectangle, com el de la figura on es coneix la hipotenusa a=100 m i l’àrea A=2400 m2. Troba:
a) La longitud de l’alçada corresponent a la hipotenusa.
b) la longitud de n
c) la longitud del catet b. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 485 › ›
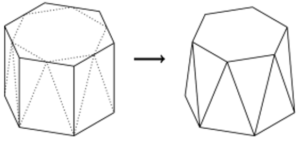
| Un prisma hexagonal regular s’escapça tal com mostra la figura.
La cara superior es converteix en un altre hexàgon regular i les 6 cares rectangulars laterals es converteixen en 12 triangles isòsceles de dues mides diferents.
Quina fracció del volum del prisma original s’ha perdut? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 484 › ›
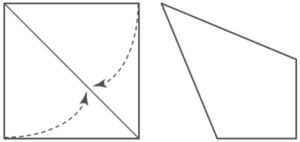
| La Maria agafa un tros quadrat de paper de costat 1 i en doblega dos dels costats cap a la diagonal com es mostra en la figura, i així s’obté un quadrilàter. Quant val l’àrea d’aquest quadrilàter? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 481 › ›
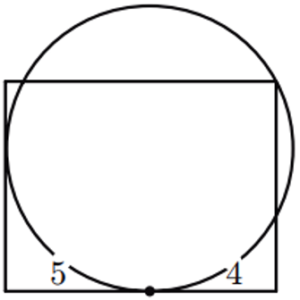
| Tenim un rectangle i un cercle que és tangent a dos dels costats del rectangle i que passa per un dels vèrtexs, com es mostra en la figura. Un dels punts de tangència és a distància 5 i 4 dels dos vèrtexs adjacents. Quant val l’àrea del rectangle? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 480 › ›
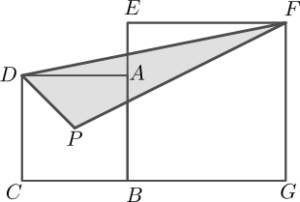
| Les diagonals dels quadrats ABCD i EFGB són 7 cm i 10 cm respectivament. El punt P és la intersecció de les diagonals del quadrat ABCD. Trobeu l’àrea del triangle FPD. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 476 › ›
|
|