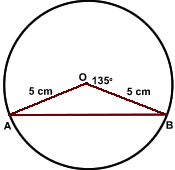
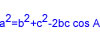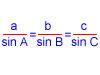| [IBO] Troba l’àrea del segment circular limitada per la corda AB |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 350 › ›
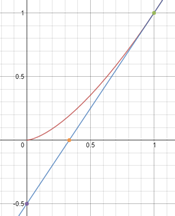
[IBO] La tangent a la corba y² – x³ = 0 al punt P(1,1), talla l’eix X a l’abcissa Q i l’eix Y a l’ordenada R.
Troba la ratio PQ/QR |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 313 › ›
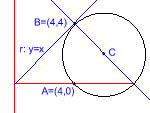
[PAAU 2001] La circumferència C passa pel punt A=(4,0) i és tangent a la recta y=x en el punt B=(4,4).
a) Determineu l’equació de la recta que passa per B i el centre de la circumferència C.
b) Trobeu el centre de C i calculeu el seu radi. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 298 › ›
[PAAU 2011] Donada la recta r:{2x-y+3z=2 i x+z=1}
a) Trobeu-ne un vector director
b) Calculeu l’equació contínua de la recta paral·lela a r que passa pel punt P=(1,0,-1) |
|
› › Clica per a veure el vídeo d’ACTIVITAT 297 › ›
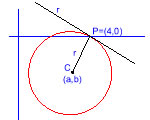
[PAAU 2000] Considereu la circumferència x² + y² – 6x + 4y + 8 =0
a) Calculeu-ne el centre i el radi
b) Comproveu que el punt P(4,0) està contingut a la circumferència i determineu l’equació de la recta tangent a aquest punt (la recta tangent en un punt d’una circumferència és la perpendicular al radi que passa per aquest punt). |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 295 › ›
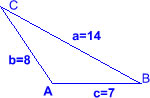
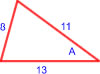
| [PAAU 2000] Els costats d’un triangle són de longituds 8 cm, 11 cm i 13 cm. Calculeu el sinus de l’angle més petit. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 293 › ›
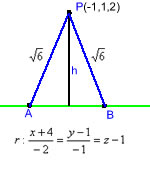
[PAAU 2010] a) Trobeu els punts A i B de la recta r: (x+4)/(-2)=(y-1)/(-1)=z-1
que estan a una distancia [arrel de 6] del punt P=(-1,1,2)
b) Trobeu l’àrea del triangle de vèrtex A, B, P |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 292 › ›
| [PAAU 2010] Trobeu l’equació general del pla que conté la recta r1: (x-1)/2 = y = 2-z i és paral·lel a la recta { x-y-z=0 x-2y+z=0} |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 291 › ›
[PAAU 2010] Siguin r i s dues rectes d’equacions:
r:(x,y,z)=(-4,3,4)+t(2,-1,1)
s:x+1=(y-2)/(-1)=(z-a)/3
a) Trobeu el valor del paràmetre ‘a’ perquè aquestes rectes es tallin
b) En el cas en què es tallin, trobeu l’equació general del pla que les conté |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 290 › ›
[PAAU 2010] Donats el punt P=(1,0,-2) i la recta r:(x-5)/2= (y-3)/2= (z+3)/(-2)
a) Trobeu l’equació contínua de la recta que passa pel punt P i talla perpendicularment la recta r
b) Calculeu la distància del punt P a la recta r |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 289 › ›
[PAAU 2010] Donats el pla 5x + y + 3z = 4 y la recta r : {ax – y = 2 , 2y + z = -3}
estudieu-ne la posició relativa en funció del paràmetre ‘a’. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 279 › ›
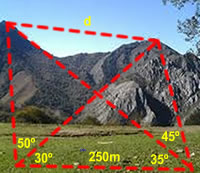
| Troba la distància entre els dos cims amb l’ajut de les triangulacions que s’indiquen a l’esquema |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 277 › ›
Demostració de la fórmula del cosinus de la suma de dos angles aguts
cos(A+B)= cosA·cosB – sinA·sinB
› › Clica per a veure el vídeo d’ACTIVITAT 276 › ›
Demostració de la fórmula del sinus de la suma de dos angles aguts
sin(A+B)= sinA·cosB + sinB·cosA
› › Clica per a veure el vídeo d’ACTIVITAT 275 › ›
[PAAU 2000] Donats els vectors u=(1,-1,4), v=(1,2,3) i w=(1,0,0)
a) Determineu si són vectors linealment depenents o independents
b) Calculeu la relació que hi ha d’haver entre els valors de a i b per tal que el vector (a,1,b) sigui combinació lineal de u i v. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 268 › ›
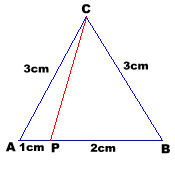
| [PAAU 2001] Siguin A, B i C els tres vèrtex d’un triangle equilàter de costat 3 cm i P el punt del costat AB qu és a 1 cm del vèrtex A. Quina és la longitud del segment CP? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 264 › ›
[PAAU 2012] Donats els punts P=(1,0,0), Q=(0,2,0) R=(0,0,3) i S=(1,2,3)
a) Calculeu l’equació general del pla que conté els punts P, Q i R
b) Comproveu si els quatre punts són coplanaris |
|
› › Clica per a veure el vídeo d’ACTIVITAT 263 › ›
|
|