Simetria Axial – Aplicació Geogebra
Els polígons de la figura presenten simetria axial. Podeu modificar el polígon ABCD i també la posició relativa de la recta, i comprovareu que l’altre polígon és el reflex del primer respecte la recta HH’
› › Clica per a veure el vídeo d’ACTIVITAT 229 › ›
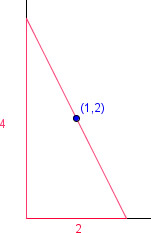
| De totes les rectes que passen pel el punt (1,2), troba la que determina amb els eixos de coordenades, en el primer quadrant, un triangle d’àrea mínima.
Aquest és un problema d’optimització que en aquest cas resolem amb una aplicació de Geogebra
També es pot resoldre buscant l’area del triangle en funció de la base, derivant l’expressió i igualant a zero per a buscar el valor de la base.
sigui x la base;
Area(x) = x2/(x-1) -> Area'(x) = (x² – 2x) / (x-1)² = 0 -> x² – 2x = 0 -> x = 2 -> Area (2)= 4 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 228 › ›
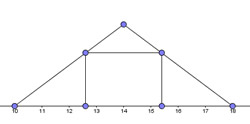
| Trobar les dimensions d’un rectangle inscrit dins un triangle isòsceles de base 8 cm i altura 3 cm.
En aquest cas el problema es resol amb una aplicació feta amb Geogebra |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 227 › ›
Geometria – Homotècies en el pla
La homotècia és una transformació geomètrica que manté la forma de la figura, de manera que els costats de la homotècia són proporcionals als de la figura original.
Llisca el cursor (des de valor 0 a 5) per tal d’obtenir una homotècia de raó determinada (els costats tenen aquesta proporció).
› › Clica per a veure el vídeo d’ACTIVITAT 225 › ›
Una hipèrbola pot ser definida com el lloc geomètric dels punts on el valor absolut de la diferència de les distàncies als dos focus és una constant igual a 2 cops la distància entre els seus dos vèrtexs.
Similar a una paràbola, una hipèrbola és una corba oberta, el que significa que continua indefinidament fins a l’infinit. Consta de dues corbes desconnectades anomenats els seus braços. Els punts en les dues branques que estan més a prop entre si es diuen vèrtexs, i el segment de línia que els connecta es diu eix major. El punt mitjà de l’eix major es coneix com a centre de la hipèrbola. A la mateixa recta de l’eix major hi ha els dos punts focals (focus) de la hipèrbola. La línia a través d’aquests cinc punts és un dels dos eixos principals de la hipèrbola, sent l’altra la bisectriu perpendicular de l’eix major. La hipèrbola té simetria de mirall al voltant dels seus eixos principals, i també és simètrica sota un gir de 180 ° al voltant del seu centre. A grans distàncies del centre, la hipèrbola s’aproxima a dues rectes, les asímptotes, que es creuen en el centre de la hipèrbola.
En alguns problemes apareix una versió simplificada de la hipèrbola, Y = 1/X, què és una hipèrbola equilàtera, en aquest cas els braços estan als quadrants I i III, els eixos de la hipèrbola són les bisectrius dels quadrants (45º), i les asímtotes, són els eixos de cordenades).
› › Clica per a veure el vídeo d’ACTIVITAT 224 › ›
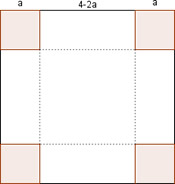
| Disposem d’una cartolina quadrada de 4 cm de costat amb la qual volem construir una capsa de base quadrada segons la imatge. Quin ha de ser el tall ‘a’ per tal que el volum sigui el màxim possible?
Aquest problema es pot resoldre derivant l’expressió del volum en funció de ‘a’ i igualant a zero, però en aquest cas es fa amb una aplicació de geogebra.
V(a)=(4 – 2a)·(4 – 2a)·a = 4a3 – 16a2 + 16a –> V'(a)= 12a2 – 16a + 16 = 0
a= 2/3 cm –> Vmax=4,74 cm3
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 223 › ›
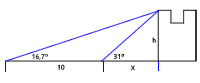
| Veiem el cim d’una torre sota un angle de 16,7º, avancem 10 m i aleshores el veiem sota un angle de 31º. Es demana la distància des del punt inicial a la base de la torre i la seva alçada |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 221 › ›
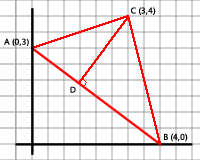
| Troba la superfície del triangle que té per vèrtexs els punts A(0,3) B(4,0) i C (3,4) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 220 › ›
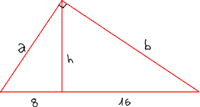
| Donat el triangle rectangle de la figura en el qual s’ha representat l’altura sobre la hipotenusa. Trobar els costats i l’altura, i demostrar que, aplicant el teorema de Pitàgores, els triangles que apareixen són tots tres rectangles. [Teorema del catet – Teorema de l’altura] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 216 › ›
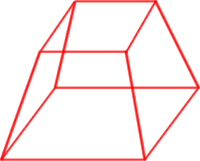
| Calcula el volum i superfície d’un tronc de piràmide de base quadrada, amb costat de la base inferior 8 cm i costat de la base superior 4 cm. L’altura del tronc és de 5 cm. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 214 › ›
| Comprova si els punts A(-3,-2), B(0,1), C(4,5) estan o no alineats |
|
› › Clica per a veure el vídeo d’ACTIVITAT 211 › ›
| [PAAU 2001]Els tres costats d’un triangle mesuren 3 cm, 4 cm i 5 cm . Calculeu els seus angles i la seva àrea. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 200 › ›
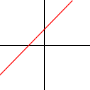
| Donada la recta y= 3x – 2, escriu la seva expressió en forma vectorial. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 180 › ›
| Donats els punts A(-2,-1) i B (1,5) troba l’equació de la recta que passa per aquests punts en forma: vectorial, paramètrica, continua, punt pendent, i explícita |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 179 › ›
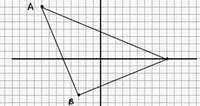
| Donats els punts A(-8,7), B(-3,-5), i C(9,0), que són els vèrtex d’un triangle i utilitzant vectors i les seves propietats, doneu tota la informació possible sobre aquest polígon. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 133 › ›
|
|