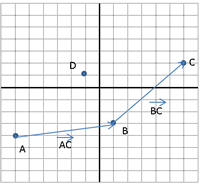
| Siguin els punts A(−6 , −4), B (1, −3), C (6 , 2) i D(x , y)
a) Calcula les coordenades del punt D sabent que el quadrilàter ABCD és un paral·lelogram.
b) Demostra que aquest paral·lelogram és un rombe.
c) Troba l’àrea i el perímetre. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 437 › ›
Troba un vector de mòdul 15 que sigui ortogonal al vector v = (48 , 14).
› › Clica per a veure el vídeo d’ACTIVITAT 436 › ›
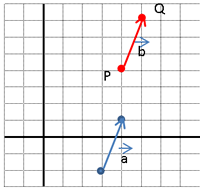
| El vector a té l’origen en el punt (3,−2) i l’extrem en el punt (4, 1). El vector s, equipol·lent a l’anterior, té origen en el punt P (4, 4). Troba’n les coordenades Q de l’extrem. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 435 › ›
Busca el valor de k perquè els vectors u = (1 , 2) i v = ( k , 1) formin un angle de 30°
› › Clica per a veure el vídeo d’ACTIVITAT 434 › ›
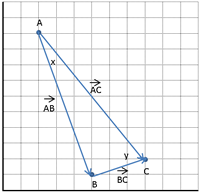
| Demostra que el triangle de vèrtexs els punts A(2 , 10), B (5 , 1) i C (8 , 2) és rectangle en B. Quant mesuren els altres dos angles del triangle? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 433 › ›
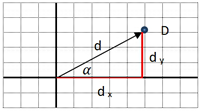
| Calcula les coordenades cartesianes dels punts M, S, els vectors de posició dels quals són m= 430º i s=√3330º |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 432 › ›
| Expressa en forma polar el vector posició de cadascun dels punts següents A (-√8, √8) i B (6,-8) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 431 › ›
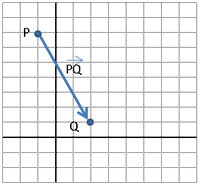
| El vector PQ = (3,−6) té l’extrem en el punt Q (2, 1). Determina les coordenades de l’origen P i el mòdul d’aquest vector. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 430 › ›
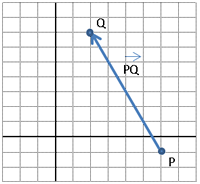
| El vector PQ =(−4, 8) té l’origen en el punt P (6, −1).
Determina les coordenades de l’extrem Q i el mòdul d’aquest vector. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 429 › ›
Calcula a·a sabent que a·b = 18, b·b = 27 i l’angle entre els vectors a i b és de 30°.
› › Clica per a veure el vídeo d’ACTIVITAT 427 › ›
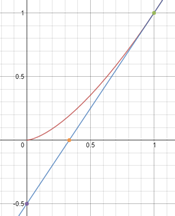
[IBO] La tangent a la corba y² – x³ = 0 al punt P(1,1), talla l’eix X a l’abcissa Q i l’eix Y a l’ordenada R.
Troba la ratio PQ/QR |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 313 › ›
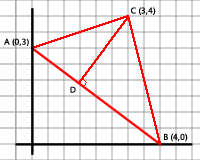
| Troba la superfície del triangle que té per vèrtexs els punts A(0,3) B(4,0) i C (3,4) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 220 › ›
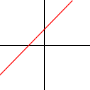
| Donada la recta y= 3x – 2, escriu la seva expressió en forma vectorial. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 180 › ›
| Donats els punts A(-2,-1) i B (1,5) troba l’equació de la recta que passa per aquests punts en forma: vectorial, paramètrica, continua, punt pendent, i explícita |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 179 › ›
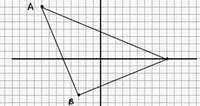
| Donats els punts A(-8,7), B(-3,-5), i C(9,0), que són els vèrtex d’un triangle i utilitzant vectors i les seves propietats, doneu tota la informació possible sobre aquest polígon. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 133 › ›
|
|


















