| En uns grans magatzems han de determinar el preu de venda d’un jersei. Un estudi de mercat indica que si el preu és de 75 € es vendran 100 jerseis. També es pot pensar que per cada 5 € d’augment en el preu es vendran 20 jerseis menys, i que, en canvi, per cada 5 € que s’abaixi el preu es vendran 20 jerseis més.Suposant que es fabriquen tants jerseis com se’n venen i que el preu de cost de cadascun és de 30 €, quin serà el preu de venda que donarà uns beneficis màxims? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 599 › ›
| Un robot surt des de l’origen de coordenades i circula amb moviment rectilini uniforme cap a la dreta de l’eix d’abscisses, a una velocitat de 50 m/s. Un segon després surt un altre robot del mateix punt i que circula com el primer, però 1 m/s més ràpid. I així, successivament, cada segon va sortint un altre robot des de l’origen de coordenades cap a la dreta de l’eix d’abscisses, que circula 1 m/s més ràpid que l’immediatament anterior. El darrer robot comença a circular 50 segons després del primer i, per tant, a una velocitat de 100 m/s. Quina és la velocitat del robot que va al capdavant de la fila de robots 100 segons després que hagi sortit el primer robot? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 541 › ›
| Una casa de 200 m2 es troba en una parcela, la distància a esquerra i dreta entre la tanca i la casa ha de ser de 3m i la distància a dalt i abaix ha de ser de 10 m. Quina és l’àrea mínima de la parcela, i la seva amplada |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 465 › ›
| Determina les mides d’una finestra d’arc de mig punt, sabent que el perímetre ha de ser de 10 m si es vol obtenir la superfície màxima. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 460 › ›
| Es vol construir una porteria de futbol amb un llistó de 16 metres de longitud. Quines són les mides que fan l’àrea més gran. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 459 › ›
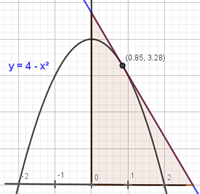
| En quin punt de la paràbola y = 4 – x2 la tangent forma amb els eixos de coordenades un triangle d’area mínima? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 441 › ›
| En quin punt de la paràbola y = 4 – x2 la tangent forma amb els eixos de coordenades un triangle d’area mínima? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 440 › ›
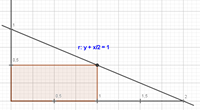
| De entre tots els rectangles situats en el primer quadrant que tenen dos dels seus costats sobre els eixos de coordenades i un vèrtex sobre la recta y + x/2 = 1, troba el que té la superfíciemes gran. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 439 › ›
| Una finestra té una superfície de 1 m2. Si el cost de l’amplada de la finestra és de 12,5 €/m i el cost de l’altura de la finestra és de 8 €/m. Troba les mides que aconsegueixen el preu més baix. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 438 › ›
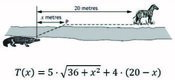
Un cocodril vol capturar una zebra que està 20m més endavant però a l’altra banda del riu. El cocodril viatja a diferent velocitat a l’aigua i a terra. El temps que triga el cocodril en atrapar la zebra ve donat per la fórmula de la dreta.
Estudia 3 situacions:
1 – El cocodril no viatja per terra i segueix una línia recta a través del riu fins a atrapar-la
2 – El cocodril viatja, per l’aigua, la distància més curta possible
3 – Entre els temps que s’han obtingut en els casos anteriors hi ha un valor de x que minimitza el temps que triga el cocodril en atrapar la presa. Troba’l i digues quin és aquest temps. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 310 › ›
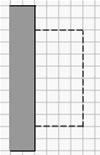
Amb 200 m de filferro volem construir una tanca rectangular per a guardar el bestiar. Per tal de fer-la més gran aprofitarem la pared lateral de la masia, de manera que amb el filferro només caldrà fer 3 dels 4 costats, essent la paret el 4t costat.
Es demana trobar les dimensions del rectangle per tal d’obtenir la superfície màxima. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 237 › ›
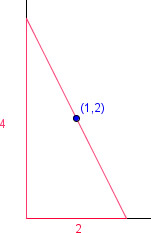
| De totes les rectes que passen pel el punt (1,2), troba la que determina amb els eixos de coordenades, en el primer quadrant, un triangle d’àrea mínima.
Aquest és un problema d’optimització que en aquest cas resolem amb una aplicació de Geogebra
També es pot resoldre buscant l’area del triangle en funció de la base, derivant l’expressió i igualant a zero per a buscar el valor de la base.
sigui x la base;
Area(x) = x2/(x-1) -> Area'(x) = (x² – 2x) / (x-1)² = 0 -> x² – 2x = 0 -> x = 2 -> Area (2)= 4 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 228 › ›
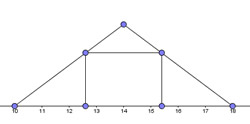
| Trobar les dimensions d’un rectangle inscrit dins un triangle isòsceles de base 8 cm i altura 3 cm.
En aquest cas el problema es resol amb una aplicació feta amb Geogebra |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 227 › ›
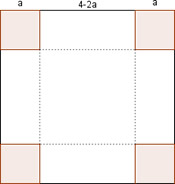
| Disposem d’una cartolina quadrada de 4 cm de costat amb la qual volem construir una capsa de base quadrada segons la imatge. Quin ha de ser el tall ‘a’ per tal que el volum sigui el màxim possible?
Aquest problema es pot resoldre derivant l’expressió del volum en funció de ‘a’ i igualant a zero, però en aquest cas es fa amb una aplicació de geogebra.
V(a)=(4 – 2a)·(4 – 2a)·a = 4a3 – 16a2 + 16a –> V'(a)= 12a2 – 16a + 16 = 0
a= 2/3 cm –> Vmax=4,74 cm3
|
 |
› › Clica per a veure el vídeo d’ACTIVITAT 223 › ›
|
|