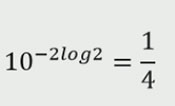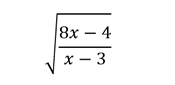| [VARIACIONS AMB REPETICIÓ, COMBINACIONS] Què és més fàcil d’endevinar: una travessa de 14 encerts o la loteria primitiva? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 341 › ›
[TEOREMA DE BAYES] S’ha fet una estadística amb tots els jugadors de futbol de la ciutat, i s’ha arribat a la següent conclusió:
El 40% són davanters, i d’aquestos el 50% són els capitans de l’equip
El 35% són migcampistes, i d’aquestos el 40% són els capitans de l’equip
El 20% són defenses, i d’aquestos el 30% són els capitans de l’equip
El 5% són porters, i d’aquestos el 20% són els capitans de l’equip
Quina probabilitat hi ha que al entrevistar un jugador de futbol de la ciutat que sigui el capità de l’equip, aquest jugui de davanter?
› › Clica per a veure el vídeo d’ACTIVITAT 340 › ›
[PROBABILITAT TOTAL] S’ha fet una estadística amb tots els jugadors de futbol de la ciutat, i s’ha arribat a la següent conclusió:
El 40% són davanters, i d’aquestos el 50% són els capitans de l’equip
El 35% són migcampistes, i d’aquestos el 40% són els capitans de l’equip
El 20% són defenses, i d’aquestos el 30% són els capitans de l’equip
El 5% són porters, i d’aquestos el 20% són els capitans de l’equip
Quina probabilitat hi ha que al entrevistar un jugador de futbol de la ciutat, aquest sigui el capità de l’equip?
› › Clica per a veure el vídeo d’ACTIVITAT 339 › ›
[TEOREMA DE BAYES] En una classe el 40% dels alumnes són nois, i a un 80% dels nois els hi agraden els cotxes. A les noies només un 30% els hi agraden els cotxes.
Quina probabilitat hi ha de què triat un alumne qualsevol que li agradin els cotxes, aquest sigui un noi?
› › Clica per a veure el vídeo d’ACTIVITAT 338 › ›
[PROBABILITAT TOTAL] En una classe el 40% dels alumnes són nois, i a un 80% dels nois els hi agraden els cotxes. A les noies només un 30% els hi agraden els cotxes.
Quina probabilitat hi ha de què triat un alumne qualsevol li agradin els cotxes?
› › Clica per a veure el vídeo d’ACTIVITAT 337 › ›
[VARIACIONS AMB REPETICIÓ I SENSE REPETICIÓ] Amb les xifres 1, 2 i 3 quants números de 5 xifres es poden escriure?
a) Sense repetir xifres. Quants d’aquests números són parells?
b) Repetint xifres. Quants d’aquests números són parells?
Amb les xifres 1, 2, 3, 4 i 5 quants números de 3 xifres es poden escriure?
a) Sense repetir xifres. Quants d’aquests números són parells?
b) Repetint xifres. Quants d’aquests números són parells?
› › Clica per a veure el vídeo d’ACTIVITAT 336 › ›
[VARIACIONS AMB REPETICIÓ] Quants números cap-i-cua de 5 xifres es poden escriure?
I si tenen 6 xifres?
› › Clica per a veure el vídeo d’ACTIVITAT 335 › ›
[PERMUTACIONS AMB REPETICIÓ]En una prestatgeria hi caben 10 llibres. N’hi ha 5 de matemàtiques, 3 de física i 2 de química. (Els llibres de cada matèria són iguals) De quantes maneres es poden ordenar?
I si canviem un llibre de matemàtiques per un de medi natural?
I si tots deu llibres són diferents? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 334 › ›
[PERMUTACIONS] En una parada de autobús estan esperant 3 amigues i altres 3 persones.
De quantes maneres poden seure tots plegats si les 3 amiguen volen estar juntes?
› › Clica per a veure el vídeo d’ACTIVITAT 333 › ›
[PERMUTACIONS] De quantes maneres diferents poden fer una fila 3 nois i 4 noies, si no hi poden haver dues noies juntes?
I si hi ha 3 noies i 3 nois?
› › Clica per a veure el vídeo d’ACTIVITAT 332 › ›
[COMBINACIONS SENSE REPETICIÓ] A una reunió assisteixen 10 persones, quantes encaixades de mans es donaran?
Si seuen per a dinar en dues taules diferents de 5 places, de quantes maneres diferents poden seure, si la posició que ocupen en cada taula és indiferent?
› › Clica per a veure el vídeo d’ACTIVITAT 331 › ›
[PERMUTACIONS AMB REPETICIÓ I SENSE REPETICIÓ] De quantes maneres diferents es poden ordenar les lletres de la paraula ARMARI?
I de la paraula SALSA?
I de la paraula PROBLEMA?
› › Clica per a veure el vídeo d’ACTIVITAT 330 › ›
[COMBINACIONS AMB REPETICIÓ I SENSE REPETICIÓ] A la nevera hi ha 6 tipus de begudes, de quantes maneres podem agafar 4 ampolles:
a) Si es poden repetir les begudes
b) Si no es poden repetir les begudes
› › Clica per a veure el vídeo d’ACTIVITAT 329 › ›
[PERMUTACIONS CIRCULARS I PERMUTACIONS ORDINÀRIES] De quantes maneres poden seure 6 persones en una taula rodona?
I si seuen a la barra d’un bar?
› › Clica per a veure el vídeo d’ACTIVITAT 328 › ›
| Un jugador de bàsquet encistella de promitg un 80% dels cops que llença a cistella. Llença tres tirs lliures. Troba quina és la probabilitat de què …
a) encistelli 3 cops seguits.
b) encistelli almenys un cop?
c) encistelli un sol cop?
d) encistelli dos cops? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 327 › ›
Justifica si són dependents o independents, compatibles o incompatibles, els successos x i y en els següents casos:
a) p(x) = 1/5, p(y) = 3/5, P(x U y) = 4/5
b) p(x) = 1/3, p(y) = 5/6, P(x U y) = 8/9
› › Clica per a veure el vídeo d’ACTIVITAT 326 › ›
| Demostra si es certa o no la igualtat de la imatge |
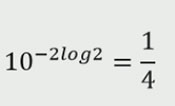 |
› › Clica per a veure el vídeo d’ACTIVITAT 325 › ›
En una classe al 80% dels alumnes els hi agrada el futbol. I al 60% els hi agrada el basquet. A un 50% els hi agraden tots dos esports. Si preguntem a un alumne qualsevol, quina és la probabilitat de què:
a) Li agradi el futbol però no el basquet
b) Li agradi el basquet però no el futbol
c) No li agradin cap dels dos esports
d) Li agradin tots dos esports si sabem que li agrada el futbol
e) No li agradi el futbol sabent que li agrada el basquet
› › Clica per a veure el vídeo d’ACTIVITAT 324 › ›
Si A i B són successos de probabilitat no nul·la, justifica si són certes les afirmacions següents:
a) Si A i B són independents, aleshores són incompatibles
a) Si A i B són incompatibles, aleshores són independents
c) Si A i B són independents, aleshores P(A) ∩ P(B)= P(A/B)·P(B/A)
› › Clica per a veure el vídeo d’ACTIVITAT 323 › ›
| Troba el conjunt de valors de x que fan que la funció de la imatge tingui valors reals |
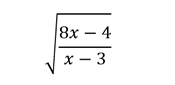 |
› › Clica per a veure el vídeo d’ACTIVITAT 322 › ›
|
|