Matemàtiques « PRoBLeMeS

ACTIVITAT 321

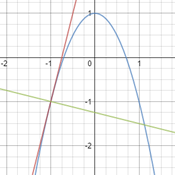
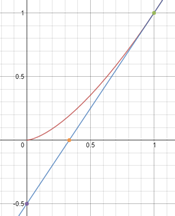
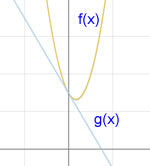
[IBO] Troba l’equació de la recta tangent a la corba y = x² que és paral·lela a la recta y = x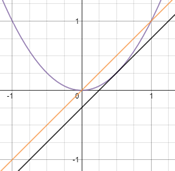

› › Clica per a veure el vídeo d’ACTIVITAT 321 › ›

ACTIVITAT 320

[IBO]Donada la corba x³·y²=8. Troba l’equació de la recta normal a la corba en el punt (2,1)

› › Clica per a veure el vídeo d’ACTIVITAT 320 › ›

[IBO] [COMBINACIONS] Hi ha 22 estudiants en una aula, dels quals 16 són noies i 6 són nois. Es seleccionen 4 estudiants per a representar-los
a) Quines possibilitats hi ha de què siguin dos nois i dues noies.
b) Quines possibilitats hi ha de què tots quatre siguin del mateix sexe.

› › Clica per a veure el vídeo d’ACTIVITAT 319 › ›

ACTIVITAT 318

[IBO] Les arrels de l’equació 2x² + 4x – 1 = 0 són a i b (no calculis l’arrel).

Quina és l’equació de 2n grau que té com a solucions a² i b²?

› › Clica per a veure el vídeo d’ACTIVITAT 318 › ›

ACTIVITAT 317

Troba l’equació de la recta tangent a la corba y = x² que és paral·lela a l’eix horitzontal, troba també l’equació de la recta perpendicular a l’anterior i que passa per x = 1

› › Clica per a veure el vídeo d’ACTIVITAT 317 › ›

ACTIVITAT 316

[IBO] Troba l’equació de la recta normal a la corba y = 1 – 2x², per x = -1

› › Clica per a veure el vídeo d’ACTIVITAT 316 › ›

ACTIVITAT 315

[IBO] Considera la recta tangent a la corba y = x³ + 4x² + x – 6
a) Troba l’equació d’aquesta recta al punt on x = -1
b) Troba les coordenades del punt on aquesta recta talla de nou la corba donada

› › Clica per a veure el vídeo d’ACTIVITAT 315 › ›

ACTIVITAT 314

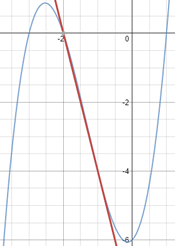
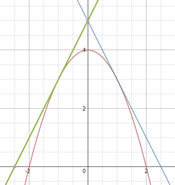
La recta y = 16x – 9 és tangent a la corba y = x³ + ax² + bx – 9 al punt (1,7).
Troba els valors de a i b

› › Clica per a veure el vídeo d’ACTIVITAT 314 › ›

ACTIVITAT 313

[IBO] La tangent a la corba y² – x³ = 0 al punt P(1,1), talla l’eix X a l’abcissa Q i l’eix Y a l’ordenada R.
Troba la ratio PQ/QR

› › Clica per a veure el vídeo d’ACTIVITAT 313 › ›

ACTIVITAT 312

[IBO] Per a quins valors de m la recta y = mx + 5, és tangent a la paràbola y = 4 – x² ?

› › Clica per a veure el vídeo d’ACTIVITAT 312 › ›

ACTIVITAT 311

[IBO] Hi ha 25 fitxes en una bossa, de les quals un nombre indeterminat són de color negre i la resta blanques. Si la probabilitat de treure consecutivament dues fitxes negres i la probabilitat de treure consecutivament una fitxa negra i una blanca, són idèntiques; quantes fitxes negres hi deu haver a la bossa?

› › Clica per a veure el vídeo d’ACTIVITAT 311 › ›

ACTIVITAT 310

Un cocodril vol capturar una zebra que està 20m més endavant però a l’altra banda del riu. El cocodril viatja a diferent velocitat a l’aigua i a terra. El temps que triga el cocodril en atrapar la zebra ve donat per la fórmula de la dreta.
Estudia 3 situacions:
1 – El cocodril no viatja per terra i segueix una línia recta a través del riu fins a atrapar-la
2 – El cocodril viatja, per l’aigua, la distància més curta possible
3 – Entre els temps que s’han obtingut en els casos anteriors hi ha un valor de x que minimitza el temps que triga el cocodril en atrapar la presa. Troba’l i digues quin és aquest temps.