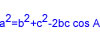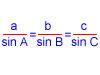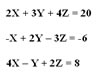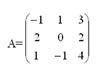En una taula hi ha dos calaixos, en un d’ells hi ha una 4 retoladors vermells i dos de blaus. A l’altre calaix hi ha 3 retoladors vermells i 3 de blaus.
Quina és la probabilitat de què en obrir un calaix s’hagi agafat un retolador vermell? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 280 › ›
[PAAU 2010] Donats el pla 5x + y + 3z = 4 y la recta r : {ax – y = 2 , 2y + z = -3}
estudieu-ne la posició relativa en funció del paràmetre ‘a’. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 279 › ›
Tenim un dau de sis cares numerades de l’1 al 6 que està manipulat i sabem del cert que la probabilitat de què surti un 6 es 3 cops més gran que qualsevol altre número.
Quina és la probabilitat de cada cara? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 278 › ›
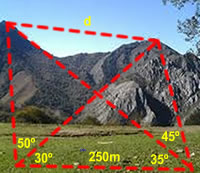
| Troba la distància entre els dos cims amb l’ajut de les triangulacions que s’indiquen a l’esquema |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 277 › ›
Demostració de la fórmula del cosinus de la suma de dos angles aguts
cos(A+B)= cosA·cosB – sinA·sinB
› › Clica per a veure el vídeo d’ACTIVITAT 276 › ›
Demostració de la fórmula del sinus de la suma de dos angles aguts
sin(A+B)= sinA·cosB + sinB·cosA
› › Clica per a veure el vídeo d’ACTIVITAT 275 › ›
| Traiem dues cartes simultàniament d’una baralla. Quina és la probabilitat de que siguin dues figures? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 272 › ›
| En una bossa fiquem sis boles amb les lletres P,R,I,M,E,R,; i les traiem una darrera l’altra. Quina és la probabilitat d’obtenir la paraula PRIMER? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 271 › ›
En una classe el 60% dels alumnes ha aprovat les matemàtiques, el 80% ha aprovat l’anglès. Un 45% del total ha aprovat tant les matemàtiques com l’anglès.
Quin percentatge d’alumnes no ha aprovat ni les matemàtiques ni l’anglès? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 270 › ›
| Donat el sistema d’equacions de la imatge troba la solució aplicant la regla de Cramer |
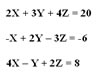 |
› › Clica per a veure el vídeo d’ACTIVITAT 269 › ›
[PAAU 2000] Donats els vectors u=(1,-1,4), v=(1,2,3) i w=(1,0,0)
a) Determineu si són vectors linealment depenents o independents
b) Calculeu la relació que hi ha d’haver entre els valors de a i b per tal que el vector (a,1,b) sigui combinació lineal de u i v. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 268 › ›
| Com es calcula un determinant pel mètode Sarrus i pel menor complementari |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 266 › ›
[PAAU 2000] Donat el sistema d’equacions
3x – 2y + z = 5
2x – 3y + z = 4
a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
b) Afegiu-hi una equació lineal de manera que el sistema resultant sigui compatible indeterminat. Resoleu el sistema que s’obtingui. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 265 › ›
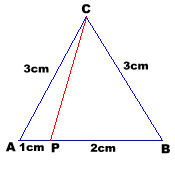
| [PAAU 2001] Siguin A, B i C els tres vèrtex d’un triangle equilàter de costat 3 cm i P el punt del costat AB qu és a 1 cm del vèrtex A. Quina és la longitud del segment CP? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 264 › ›
[PAAU 2012] Donats els punts P=(1,0,0), Q=(0,2,0) R=(0,0,3) i S=(1,2,3)
a) Calculeu l’equació general del pla que conté els punts P, Q i R
b) Comproveu si els quatre punts són coplanaris |
|
› › Clica per a veure el vídeo d’ACTIVITAT 263 › ›
Calcula el volum i superfície lateral de la barra de xocolata que veus a la fotografia
Suposa que la cara lateral correspon a un triangle equilàter de costat 4 cm i la llargada de la barra de xocolata és de 25 cm |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 262 › ›
| Calcula la superfície de la zona acolorida en blau que està continguda dins d’un quadrat de costat 10 cm |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 261 › ›
|
|