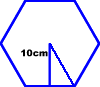
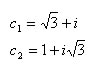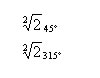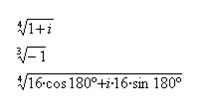| Troba la superfície d’un hexàgon regular, sabent que l’apotema val 10 cm (De pas troba l’angle central i interior de l’hexàgon regular) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 260 › ›
| Donada la funció quadràtica que veus a la dreta de l’enunciat, es demana: trobar el vèrtex, indicant si es tracta d’un màxim o d’un mínim, els intervals de creixement i decreixement, si és còncava o convexa, els punts de tall (si n’hi ha) amb l’eix horitzontal i el punt de tall amb l’eix vertical, i una representació gràfica de la funció. |
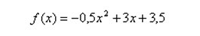 |
› › Clica per a veure el vídeo d’ACTIVITAT 259 › ›
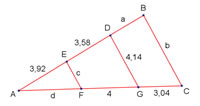
| Aplicant el Teorema de Thales i les propietats dels triangles semblants, troba el valor dels segments: a, b, c, d |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 258 › ›
Les piràmides de Kheops i Kefren són piràmides de base quadrada que tenen per amplada i altura respectivament: Kheops (230,35m ample, 146,6m altura) Kefren (215,25m ample i 143,5m altura).
1 – Calcula l’apotema lateral i l’aresta lateral de les piràmides
2 – Calcula la inclinació de la cara lateral
3 – Si la piràmide de Kefren tingués l’altura de la de Kheops (146,6m) però volguéssim que mantingués les proporcions originals quina hauria de ser la nova altura
4 – Si volguéssim que la piràmide de Kheops tingués les proporcions de la piàmide de Kefren però mantenint la seva amplada (230,35m) quina altura hauria de tenir |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 257 › ›
Troba la hipotenusa del triangle que té per catets 3 i 4
Troba el catet del triangle que té per hipotenusa 4,5 i l’altre catet val 2 |
|
› › Clica per a veure el vídeo d’ACTIVITAT 256 › ›
| Troba el valor que ha de tenir la hipotenusa d’un triangle si sabem que un catet és el doble de gran que l’altre. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 255 › ›
Comprova si els triangles que tenen per costats:
a) 5, 12, 13
b) 3, 4, 6
c) 4, 9, 9
són o no triangles rectangles |
|
› › Clica per a veure el vídeo d’ACTIVITAT 254 › ›
Tenim un pot de pilotes de tennis com el de la imatge, podem suposar que les pilotes ajusten perfectament (no hi ha espai lliure entre les pilotes i el lateral del cilindre, ni entre les pilotes i la base i la tapa).
Sabem que el diàmetre d’una pilota de tennis és de 6,2 cm.
Ens demanen que trobem, el volum del pot que no està ocupat per les pilotes |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 253 › ›
Raonament sobre la relació d’angles complementaris, suplementaris, oposats, i amb diferència de 90º i 180º
› › Clica per a veure el vídeo d’ACTIVITAT 252 › ›
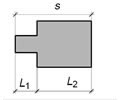
| Les peces d’una màquina estan representades en un plànol. Una determinada peça de la màquina mesura 1,2 mm, però en el plànol aquesta longitud és de 15 cm. Ens demanen trobar l’escala del plànol. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 250 › ›
Desconeixem l’escala a la que està fet un plànol, en canvi sabem que la distància entre dos punts d’aquest plànol és de 3 cm i que a la realitat aquesta distància és de 15 Km. Es demana trobar l’escala d’aquest plànol.
› › Clica per a veure el vídeo d’ACTIVITAT 249 › ›
| Desconeixem l’escala a la que està fet un plànol, en canvi sabem que la distància entre dos punts d’aquest plànol és de 3 cm i que a la realitat aquesta distància és de 15 Km. Es demana trobar l’escala d’aquest plànol. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 248 › ›
| Tenim un plànol a escala 1:1500000 que correspon a una determinada zona geogràfica. Sabem que la distànica entre dues ciutats d’aquesta zona és de 75 Km. Es demana trobar la distància equivalent al plànol |
|
› › Clica per a veure el vídeo d’ACTIVITAT 247 › ›
| Multiplica i divideix entre si, els números complexos C1 i C2, tant en format binòmic com en format polar i comprova que els resultats obtinguts són els mateixos |
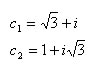 |
› › Clica per a veure el vídeo d’ACTIVITAT 246 › ›
| Troba el número complex tal que el seu quadrat coincidexi amb el seu conjugat |
|
› › Clica per a veure el vídeo d’ACTIVITAT 245 › ›
| Troba una equació de segon grau que tingui per solucions els números complexos que veus indicats a la pantalla |
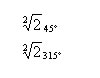 |
› › Clica per a veure el vídeo d’ACTIVITAT 244 › ›
| Calcula les arrels complexes que veus indicades a la pantalla |
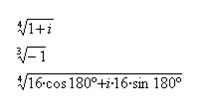 |
› › Clica per a veure el vídeo d’ACTIVITAT 243 › ›
| Calcula en forma binòmica i en forma polar (1 – i)5. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 242 › ›
Operacions bàsiques amb números complexos: Suma , resta, multiplicació i divisió :
C1= 2 + 5i
C2= 3 – 4i |
|
› › Clica per a veure el vídeo d’ACTIVITAT 241 › ›
|
|