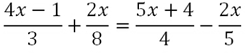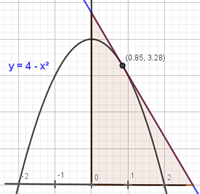
| En quin punt de la paràbola y = 4 – x2 la tangent forma amb els eixos de coordenades un triangle d’area mínima? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 441 › ›
| En quin punt de la paràbola y = 4 – x2 la tangent forma amb els eixos de coordenades un triangle d’area mínima? |
|
› › Clica per a veure el vídeo d’ACTIVITAT 440 › ›
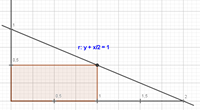
| De entre tots els rectangles situats en el primer quadrant que tenen dos dels seus costats sobre els eixos de coordenades i un vèrtex sobre la recta y + x/2 = 1, troba el que té la superfíciemes gran. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 439 › ›
| Una finestra té una superfície de 1 m2. Si el cost de l’amplada de la finestra és de 12,5 €/m i el cost de l’altura de la finestra és de 8 €/m. Troba les mides que aconsegueixen el preu més baix. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 438 › ›
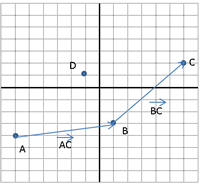
| Siguin els punts A(−6 , −4), B (1, −3), C (6 , 2) i D(x , y)
a) Calcula les coordenades del punt D sabent que el quadrilàter ABCD és un paral·lelogram.
b) Demostra que aquest paral·lelogram és un rombe.
c) Troba l’àrea i el perímetre. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 437 › ›
Troba un vector de mòdul 15 que sigui ortogonal al vector v = (48 , 14).
› › Clica per a veure el vídeo d’ACTIVITAT 436 › ›
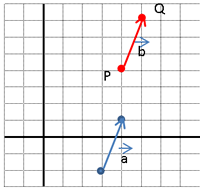
| El vector a té l’origen en el punt (3,−2) i l’extrem en el punt (4, 1). El vector s, equipol·lent a l’anterior, té origen en el punt P (4, 4). Troba’n les coordenades Q de l’extrem. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 435 › ›
Busca el valor de k perquè els vectors u = (1 , 2) i v = ( k , 1) formin un angle de 30°
› › Clica per a veure el vídeo d’ACTIVITAT 434 › ›
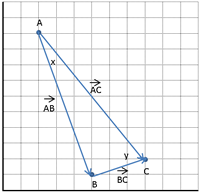
| Demostra que el triangle de vèrtexs els punts A(2 , 10), B (5 , 1) i C (8 , 2) és rectangle en B. Quant mesuren els altres dos angles del triangle? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 433 › ›
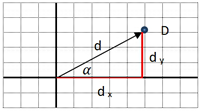
| Calcula les coordenades cartesianes dels punts M, S, els vectors de posició dels quals són m= 430º i s=√3330º |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 432 › ›
| Expressa en forma polar el vector posició de cadascun dels punts següents A (-√8, √8) i B (6,-8) |
|
› › Clica per a veure el vídeo d’ACTIVITAT 431 › ›
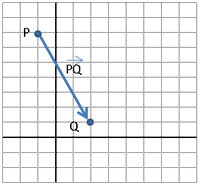
| El vector PQ = (3,−6) té l’extrem en el punt Q (2, 1). Determina les coordenades de l’origen P i el mòdul d’aquest vector. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 430 › ›
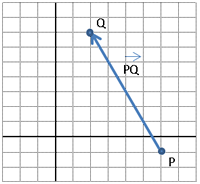
| El vector PQ =(−4, 8) té l’origen en el punt P (6, −1).
Determina les coordenades de l’extrem Q i el mòdul d’aquest vector. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 429 › ›
| 5 operaris han muntat una màquina en 12 dies treballant 8 hores diàries. Quants operaris es necessiten per muntar la mateixa màquina en 8 dies treballant 10 hores diàries
[Regla de 3 composta] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 428 › ›
Calcula a·a sabent que a·b = 18, b·b = 27 i l’angle entre els vectors a i b és de 30°.
› › Clica per a veure el vídeo d’ACTIVITAT 427 › ›
| Una persona recorre 420 km en 10 dies caminant 8 hores diàries. Quina distància recorreria en un any caminant 5 hores diàries?
[Regla de 3 composta] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 426 › ›
| 5 pintors pinten 14 metres de paret en 9 hores. Quantes hores trigaran 7 pintors en pintar una paret de 15 metres?
[Regla de 3 composta] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 425 › ›
| Cinc aixetes omplen un dipòsit de 450 litres en 9 hores. Quan trigaran 12 aixetes en omplir un dipòsit de 600 litres?
[Regla de 3 composta] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 424 › ›
| 3 gats cacen 3 ratolins en 3 minuts. Quants gats faran falta per a caçar 10 raolins en 10 minuts
[Regla de tres composta] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 423 › ›
| Fes la multiplicació (3x4 + 3x2 -2x + 1) · (2x2 -3x +4) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 421 › ›
|
|
