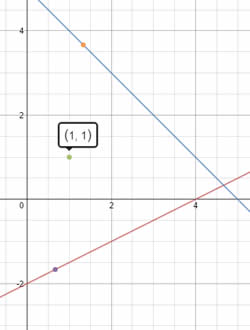
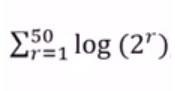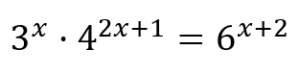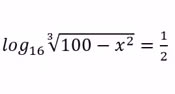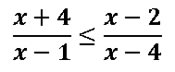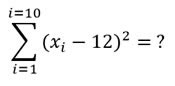| [IBO] El gràfic mostra les rectes x + y = 5 i x – 2y – 4 = 0, i també el punt P (1,1). És dibuixa una recta que passant per P talli les dues rectes anteriors pels punts R i Q respectivament, de manera que P sigui el punt mig del segment RQ. Es demana trobar les coordenades dels punts R i Q |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 371 › ›
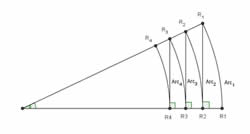
| [IBO] Troba la suma infinita dels arcs de la imatge, suposant R1=1 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 370 › ›
[IBO] La suma dels n primers termes d’una progressió aritmètica ve donada per Sn=2n2 – n, on n és un enter
- Troba els 3 primers termes de la progressió
- Troba l’expressió de an
› › Clica per a veure el vídeo d’ACTIVITAT 369 › ›
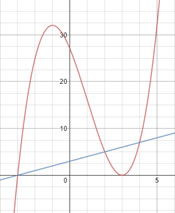
| [IBO] Troba l’àrea total de les dues regions compreses entre la corva y = x3 – 3x2 – 9x + 27 i la recta y = x + 3 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 368 › ›
| [IBO] Calcula l’expressió de la imatge en funció de a·log 2. On a és un número racional |
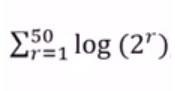 |
› › Clica per a veure el vídeo d’ACTIVITAT 367 › ›
[IBO] Els termes a, 1, b estan en progressió aritmètica. Els termes 1, a, b estan en progressió geomètrica. Troba els valors: a i b, a≠b
› › Clica per a veure el vídeo d’ACTIVITAT 364 › ›
[IBO] Els processos independents A i B són tals que P(A)=0,4 i P(AUB)=0,88. Troba:
a) P(B)
b) La probabilitat que succeeixi A o B, però no tots dos alhora
› › Clica per a veure el vídeo d’ACTIVITAT 363 › ›
| [IBO] Donat el cercle x² + (y – 2)² = 1, trobeu els possibles pendents de la recta y=kx, tal que sigui tangent al cercle. |
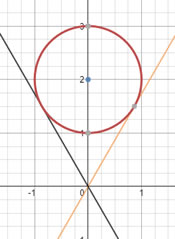 |
› › Clica per a veure el vídeo d’ACTIVITAT 362 › ›
[IBO] Troba els valors que pot tenir k, perquè les solucions a i b de l’equació x² – kx + (k+1) = 0, compleixin que a² + b² = 13
› › Clica per a veure el vídeo d’ACTIVITAT 361 › ›
| [IBO] Troba el vèrtex de la funció f(x)=x² -6x +5, explicant les transformacions que ha sofert la funció a partir de f(x)=x² |
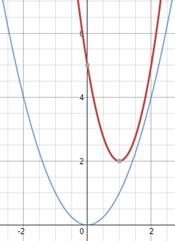 |
› › Clica per a veure el vídeo d’ACTIVITAT 360 › ›
| [IBO][PERMUTACIONS]En una prestatgeria i ha 3 llibres de matemàtiques, 5 d’anglès, 4 de ciències i un diccionari.
a) De quantes maneres es poden disposar si els llibres de cada matèria han d’estar junts?
b) I si a més el diccionari ha d’estar al costat dels llibres de matemàtiques? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 359 › ›
[IBO] Determina els paràmetres a, b. a≠0, que fan (1 + x)5·(1 + ax)6 = 1 + bx + 10x²+ ….
› › Clica per a veure el vídeo d’ACTIVITAT 358 › ›
| [IBO] Determina per quins valors de x, es compleix la desigualtat de la imatge |
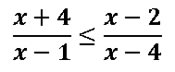 |
› › Clica per a veure el vídeo d’ACTIVITAT 357 › ›
| [IBO] La mitjana de 10 números val 10, i la desviació típica val 3.
Troba el valor de l’expressió de la imatge |
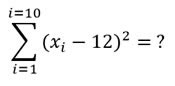 |
› › Clica per a veure el vídeo d’ACTIVITAT 355 › ›
| [IBO] Troba per quins valors de m, la desigualtat m(x+1)≤x² es compleix per a qualsevol valor de x |
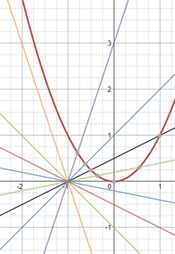 |
› › Clica per a veure el vídeo d’ACTIVITAT 354 › ›
[IBO] Troba els valors de k que fan que l’equació (1+2k)x² -10x +k-2=0 tingui solucions reals
› › Clica per a veure el vídeo d’ACTIVITAT 353 › ›
| [IBO] Un explorador mirant cap a l’est veu l’extrem d’una antena sota un angle de 35º, es desplaça 20 m, i ara mirant cap al nordest veu el cim de l’antena sota un angle de 40º. Es demana trobar l’altura de l’antena. |
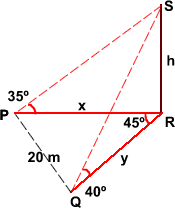 |
› › Clica per a veure el vídeo d’ACTIVITAT 352 › ›
|
|