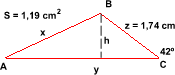
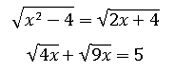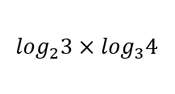| [IBO] Troba els costats i angles del triangle de la figura |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 351 › ›
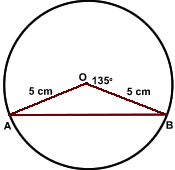
| [IBO] Troba l’àrea del segment circular limitada per la corda AB |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 350 › ›
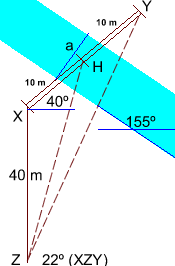
[IBO] Un pont amb un angle de 40º sobre l’horitzontal creua un riu des de X fins a Y, deixant 10 m per banda i banda del riu. Un viatjer camina des de X cap al sud 40 m fins a Z. L’angle Z, del triangle XZY és de 22º.
a) Quina longitud té el pont?
b) El riu forma amb l’horitzontal un angle de 155º, quina amplada té el riu?
c) El punt mig del pont és H, quin és l’angle Z del triangle XZH? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 349 › ›
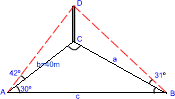
| [IBO] Un explorador camina 40 m des de la base d’una antena vertical CD, en línia recta fins a un punt A, allà comprova que la base de l’antena està a 30º sobre l’horitzontal, i l’angle d’elevació de l’antena és de 42º. Des d’A camina cap a l’est fins a un punt B, allà comprova que l’angle d’elevació de l’antena és de 31º.
a) Troba la distància AB.
b) Troba quin és l’angle al que està l’antena sobre l’horitzonal al punt B |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 348 › ›
Se sap que p(A)=0,4 i p(B)=0,5 i p(A’∩B’)=0,3
a) Troba p(AUB)
b) Troba p(A∩B)
› › Clica per a veure el vídeo d’ACTIVITAT 344 › ›
[PERMUTACIONS, VARIACIONS, COMBINACIONS] Vuit persones van de viatge en dos cotxes diferents de 4 places, com es poden distribuir si…
a) Tots tenen carnet de conduir i la plaça que ocupen a cada vehicle és indiferent?
b) Tots tenen carnet de conduir i la plaça que ocupen a cada vehicle no és indiferent?
c) Tres tenen carnet de conduir i la plaça que ocupen a cada vehicle és indiferent?
d) Tres tenen carnet de conduir i la plaça que ocupen a cada vehicle no és indiferent?
› › Clica per a veure el vídeo d’ACTIVITAT 343 › ›
[VARIACIONS AMB REPETICIÓ I SENSE REPETICIÓ]
Quants números entre 2000 i 3000 tenen les xifres diferents?
Quants números entre 2000 i 3000 contenen la xifra 5 una sola vegada?
Quants números entre 2000 i 3000 no contenen la xifra 5?
› › Clica per a veure el vídeo d’ACTIVITAT 342 › ›
| [VARIACIONS AMB REPETICIÓ, COMBINACIONS] Què és més fàcil d’endevinar: una travessa de 14 encerts o la loteria primitiva? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 341 › ›
[TEOREMA DE BAYES] S’ha fet una estadística amb tots els jugadors de futbol de la ciutat, i s’ha arribat a la següent conclusió:
El 40% són davanters, i d’aquestos el 50% són els capitans de l’equip
El 35% són migcampistes, i d’aquestos el 40% són els capitans de l’equip
El 20% són defenses, i d’aquestos el 30% són els capitans de l’equip
El 5% són porters, i d’aquestos el 20% són els capitans de l’equip
Quina probabilitat hi ha que al entrevistar un jugador de futbol de la ciutat que sigui el capità de l’equip, aquest jugui de davanter?
› › Clica per a veure el vídeo d’ACTIVITAT 340 › ›
[PROBABILITAT TOTAL] S’ha fet una estadística amb tots els jugadors de futbol de la ciutat, i s’ha arribat a la següent conclusió:
El 40% són davanters, i d’aquestos el 50% són els capitans de l’equip
El 35% són migcampistes, i d’aquestos el 40% són els capitans de l’equip
El 20% són defenses, i d’aquestos el 30% són els capitans de l’equip
El 5% són porters, i d’aquestos el 20% són els capitans de l’equip
Quina probabilitat hi ha que al entrevistar un jugador de futbol de la ciutat, aquest sigui el capità de l’equip?
› › Clica per a veure el vídeo d’ACTIVITAT 339 › ›
[TEOREMA DE BAYES] En una classe el 40% dels alumnes són nois, i a un 80% dels nois els hi agraden els cotxes. A les noies només un 30% els hi agraden els cotxes.
Quina probabilitat hi ha de què triat un alumne qualsevol que li agradin els cotxes, aquest sigui un noi?
› › Clica per a veure el vídeo d’ACTIVITAT 338 › ›
[PROBABILITAT TOTAL] En una classe el 40% dels alumnes són nois, i a un 80% dels nois els hi agraden els cotxes. A les noies només un 30% els hi agraden els cotxes.
Quina probabilitat hi ha de què triat un alumne qualsevol li agradin els cotxes?
› › Clica per a veure el vídeo d’ACTIVITAT 337 › ›
[VARIACIONS AMB REPETICIÓ I SENSE REPETICIÓ] Amb les xifres 1, 2 i 3 quants números de 5 xifres es poden escriure?
a) Sense repetir xifres. Quants d’aquests números són parells?
b) Repetint xifres. Quants d’aquests números són parells?
Amb les xifres 1, 2, 3, 4 i 5 quants números de 3 xifres es poden escriure?
a) Sense repetir xifres. Quants d’aquests números són parells?
b) Repetint xifres. Quants d’aquests números són parells?
› › Clica per a veure el vídeo d’ACTIVITAT 336 › ›
[VARIACIONS AMB REPETICIÓ] Quants números cap-i-cua de 5 xifres es poden escriure?
I si tenen 6 xifres?
› › Clica per a veure el vídeo d’ACTIVITAT 335 › ›
[PERMUTACIONS AMB REPETICIÓ]En una prestatgeria hi caben 10 llibres. N’hi ha 5 de matemàtiques, 3 de física i 2 de química. (Els llibres de cada matèria són iguals) De quantes maneres es poden ordenar?
I si canviem un llibre de matemàtiques per un de medi natural?
I si tots deu llibres són diferents? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 334 › ›
[PERMUTACIONS] En una parada de autobús estan esperant 3 amigues i altres 3 persones.
De quantes maneres poden seure tots plegats si les 3 amiguen volen estar juntes?
› › Clica per a veure el vídeo d’ACTIVITAT 333 › ›
[PERMUTACIONS] De quantes maneres diferents poden fer una fila 3 nois i 4 noies, si no hi poden haver dues noies juntes?
I si hi ha 3 noies i 3 nois?
› › Clica per a veure el vídeo d’ACTIVITAT 332 › ›
|
|