| Un jugador de bàsquet encistella de promitg un 80% dels cops que llença a cistella. Llença tres tirs lliures. Troba quina és la probabilitat de què …
a) encistelli 3 cops seguits.
b) encistelli almenys un cop?
c) encistelli un sol cop?
d) encistelli dos cops? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 327 › ›
Justifica si són dependents o independents, compatibles o incompatibles, els successos x i y en els següents casos:
a) p(x) = 1/5, p(y) = 3/5, P(x U y) = 4/5
b) p(x) = 1/3, p(y) = 5/6, P(x U y) = 8/9
› › Clica per a veure el vídeo d’ACTIVITAT 326 › ›
| Demostra si es certa o no la igualtat de la imatge |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 325 › ›
En una classe al 80% dels alumnes els hi agrada el futbol. I al 60% els hi agrada el basquet. A un 50% els hi agraden tots dos esports. Si preguntem a un alumne qualsevol, quina és la probabilitat de què:
a) Li agradi el futbol però no el basquet
b) Li agradi el basquet però no el futbol
c) No li agradin cap dels dos esports
d) Li agradin tots dos esports si sabem que li agrada el futbol
e) No li agradi el futbol sabent que li agrada el basquet
› › Clica per a veure el vídeo d’ACTIVITAT 324 › ›
Si A i B són successos de probabilitat no nul·la, justifica si són certes les afirmacions següents:
a) Si A i B són independents, aleshores són incompatibles
a) Si A i B són incompatibles, aleshores són independents
c) Si A i B són independents, aleshores P(A) ∩ P(B)= P(A/B)·P(B/A)
› › Clica per a veure el vídeo d’ACTIVITAT 323 › ›
| Troba el conjunt de valors de x que fan que la funció de la imatge tingui valors reals |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 322 › ›
| [IBO] Troba l’equació de la recta tangent a la corba y = x² que és paral·lela a la recta y = x |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 321 › ›
| [IBO]Donada la corba x³·y²=8. Troba l’equació de la recta normal a la corba en el punt (2,1) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 320 › ›
[IBO] [COMBINACIONS] Hi ha 22 estudiants en una aula, dels quals 16 són noies i 6 són nois. Es seleccionen 4 estudiants per a representar-los
a) Quines possibilitats hi ha de què siguin dos nois i dues noies.
b) Quines possibilitats hi ha de què tots quatre siguin del mateix sexe.
› › Clica per a veure el vídeo d’ACTIVITAT 319 › ›
| [IBO] Les arrels de l’equació 2x² + 4x – 1 = 0 són a i b (no calculis l’arrel).
Quina és l’equació de 2n grau que té com a solucions a² i b²? |
|
› › Clica per a veure el vídeo d’ACTIVITAT 318 › ›
| Troba l’equació de la recta tangent a la corba y = x² que és paral·lela a l’eix horitzontal, troba també l’equació de la recta perpendicular a l’anterior i que passa per x = 1 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 317 › ›
| [IBO] Troba l’equació de la recta normal a la corba y = 1 – 2x², per x = -1 |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 316 › ›
[IBO] Considera la recta tangent a la corba y = x³ + 4x² + x – 6
a) Troba l’equació d’aquesta recta al punt on x = -1
b) Troba les coordenades del punt on aquesta recta talla de nou la corba donada |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 315 › ›
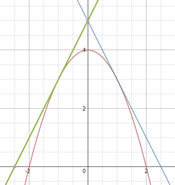
La recta y = 16x – 9 és tangent a la corba y = x³ + ax² + bx – 9 al punt (1,7).
Troba els valors de a i b
› › Clica per a veure el vídeo d’ACTIVITAT 314 › ›
[IBO] La tangent a la corba y² – x³ = 0 al punt P(1,1), talla l’eix X a l’abcissa Q i l’eix Y a l’ordenada R.
Troba la ratio PQ/QR |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 313 › ›
| [IBO] Per a quins valors de m la recta y = mx + 5, és tangent a la paràbola y = 4 – x² ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 312 › ›
[IBO] Hi ha 25 fitxes en una bossa, de les quals un nombre indeterminat són de color negre i la resta blanques. Si la probabilitat de treure consecutivament dues fitxes negres i la probabilitat de treure consecutivament una fitxa negra i una blanca, són idèntiques; quantes fitxes negres hi deu haver a la bossa?
› › Clica per a veure el vídeo d’ACTIVITAT 311 › ›
Un cocodril vol capturar una zebra que està 20m més endavant però a l’altra banda del riu. El cocodril viatja a diferent velocitat a l’aigua i a terra. El temps que triga el cocodril en atrapar la zebra ve donat per la fórmula de la dreta.
Estudia 3 situacions:
1 – El cocodril no viatja per terra i segueix una línia recta a través del riu fins a atrapar-la
2 – El cocodril viatja, per l’aigua, la distància més curta possible
3 – Entre els temps que s’han obtingut en els casos anteriors hi ha un valor de x que minimitza el temps que triga el cocodril en atrapar la presa. Troba’l i digues quin és aquest temps. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 310 › ›
| Troba la longitud d’una corda que dóna 4 voltes senceres a un cilindre de 12 cm de longitud i 4 cm de perímetre |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 309 › ›
|
|
