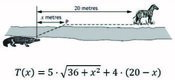
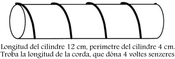
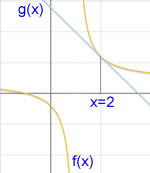
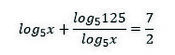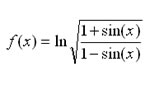PRoBLeMeS

ACTIVITAT 311

[IBO] Hi ha 25 fitxes en una bossa, de les quals un nombre indeterminat són de color negre i la resta blanques. Si la probabilitat de treure consecutivament dues fitxes negres i la probabilitat de treure consecutivament una fitxa negra i una blanca, són idèntiques; quantes fitxes negres hi deu haver a la bossa?

› › Clica per a veure el vídeo d’ACTIVITAT 311 › ›

ACTIVITAT 310

Un cocodril vol capturar una zebra que està 20m més endavant però a l’altra banda del riu. El cocodril viatja a diferent velocitat a l’aigua i a terra. El temps que triga el cocodril en atrapar la zebra ve donat per la fórmula de la dreta.
Estudia 3 situacions:
1 – El cocodril no viatja per terra i segueix una línia recta a través del riu fins a atrapar-la
2 – El cocodril viatja, per l’aigua, la distància més curta possible
3 – Entre els temps que s’han obtingut en els casos anteriors hi ha un valor de x que minimitza el temps que triga el cocodril en atrapar la presa. Troba’l i digues quin és aquest temps.

› › Clica per a veure el vídeo d’ACTIVITAT 310 › ›

ACTIVITAT 309

Troba la longitud d’una corda que dóna 4 voltes senceres a un cilindre de 12 cm de longitud i 4 cm de perímetre

› › Clica per a veure el vídeo d’ACTIVITAT 309 › ›

ACTIVITAT 308

Resol l’equació logarítmica de la imatge

› › Clica per a veure el vídeo d’ACTIVITAT 308 › ›

ACTIVITAT 307

Resol l’equació logarítmica de la imatge

› › Clica per a veure el vídeo d’ACTIVITAT 307 › ›

ACTIVITAT 306

Expressa en funció de log 2 i log 3 els logaritmes següents:
log 36
log 0,12
log 20000
log 0,5
log 25
log 1,5
log 60
log 0,006 …

› › Clica per a veure el vídeo d’ACTIVITAT 306 › ›

ACTIVITAT 305

Calculeu l’equació de la recta tangent a la corba f(x)=(x+1)/(x-1) en el punt d’abcissa x=2

› › Clica per a veure el vídeo d’ACTIVITAT 305 › ›

ACTIVITAT 304

Calculeu l’equació de la recta tangent a la corba f(x)=3x² – 2x + 3 en el punt d’abcissa x=0

› › Clica per a veure el vídeo d’ACTIVITAT 304 › ›

ACTIVITAT 303

Calculeu el valor de x que anul·la la segona derivada de la funció f(x)=e^-x²

› › Clica per a veure el vídeo d’ACTIVITAT 303 › ›

ACTIVITAT 302

Calculeu el valor de m perquè la derivada de f(x)=(mx+1)/(2x+m) per x=1 valgui -1

› › Clica per a veure el vídeo d’ACTIVITAT 302 › ›

ACTIVITAT 301

Troba la derivada de les funcions

› › Clica per a veure el vídeo d’ACTIVITAT 301 › ›

ACTIVITAT 300

Troba la derivada de la funció

› › Clica per a veure el vídeo d’ACTIVITAT 300 › ›

ACTIVITAT 299

Troba la derivada de la funció

› › Clica per a veure el vídeo d’ACTIVITAT 299 › ›

ACTIVITAT 298

[PAAU 2001] La circumferència C passa pel punt A=(4,0) i és tangent a la recta y=x en el punt B=(4,4).
a) Determineu l’equació de la recta que passa per B i el centre de la circumferència C.
b) Trobeu el centre de C i calculeu el seu radi.

› › Clica per a veure el vídeo d’ACTIVITAT 298 › ›

ACTIVITAT 297

[PAAU 2011] Donada la recta r:{2x-y+3z=2 i x+z=1}
a) Trobeu-ne un vector director
b) Calculeu l’equació contínua de la recta paral·lela a r que passa pel punt P=(1,0,-1)

› › Clica per a veure el vídeo d’ACTIVITAT 297 › ›

ACTIVITAT 296

[PAAU 2010] Donada la matriu de la imatge
a) Calculeu A² i A³
b) Deduïu el valor de A¹⁰¹

› › Clica per a veure el vídeo d’ACTIVITAT 296 › ›

ACTIVITAT 295

[PAAU 2000] Considereu la circumferència x² + y² – 6x + 4y + 8 =0
a) Calculeu-ne el centre i el radi
b) Comproveu que el punt P(4,0) està contingut a la circumferència i determineu l’equació de la recta tangent a aquest punt (la recta tangent en un punt d’una circumferència és la perpendicular al radi que passa per aquest punt).

› › Clica per a veure el vídeo d’ACTIVITAT 295 › ›