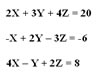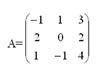| En una bossa fiquem sis boles amb les lletres P,R,I,M,E,R,; i les traiem una darrera l’altra. Quina és la probabilitat d’obtenir la paraula PRIMER? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 271 › ›
En una classe el 60% dels alumnes ha aprovat les matemàtiques, el 80% ha aprovat l’anglès. Un 45% del total ha aprovat tant les matemàtiques com l’anglès.
Quin percentatge d’alumnes no ha aprovat ni les matemàtiques ni l’anglès? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 270 › ›
| Donat el sistema d’equacions de la imatge troba la solució aplicant la regla de Cramer |
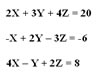 |
› › Clica per a veure el vídeo d’ACTIVITAT 269 › ›
[PAAU 2000] Donats els vectors u=(1,-1,4), v=(1,2,3) i w=(1,0,0)
a) Determineu si són vectors linealment depenents o independents
b) Calculeu la relació que hi ha d’haver entre els valors de a i b per tal que el vector (a,1,b) sigui combinació lineal de u i v. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 268 › ›
| Com es calcula un determinant pel mètode Sarrus i pel menor complementari |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 266 › ›
[PAAU 2000] Donat el sistema d’equacions
3x – 2y + z = 5
2x – 3y + z = 4
a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
b) Afegiu-hi una equació lineal de manera que el sistema resultant sigui compatible indeterminat. Resoleu el sistema que s’obtingui. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 265 › ›
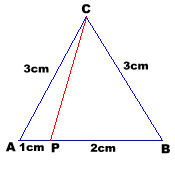
| [PAAU 2001] Siguin A, B i C els tres vèrtex d’un triangle equilàter de costat 3 cm i P el punt del costat AB qu és a 1 cm del vèrtex A. Quina és la longitud del segment CP? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 264 › ›
[PAAU 2012] Donats els punts P=(1,0,0), Q=(0,2,0) R=(0,0,3) i S=(1,2,3)
a) Calculeu l’equació general del pla que conté els punts P, Q i R
b) Comproveu si els quatre punts són coplanaris |
|
› › Clica per a veure el vídeo d’ACTIVITAT 263 › ›
Calcula el volum i superfície lateral de la barra de xocolata que veus a la fotografia
Suposa que la cara lateral correspon a un triangle equilàter de costat 4 cm i la llargada de la barra de xocolata és de 25 cm |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 262 › ›
| Calcula la superfície de la zona acolorida en blau que està continguda dins d’un quadrat de costat 10 cm |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 261 › ›
| Troba la superfície d’un hexàgon regular, sabent que l’apotema val 10 cm (De pas troba l’angle central i interior de l’hexàgon regular) |
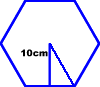 |
› › Clica per a veure el vídeo d’ACTIVITAT 260 › ›
| Donada la funció quadràtica que veus a la dreta de l’enunciat, es demana: trobar el vèrtex, indicant si es tracta d’un màxim o d’un mínim, els intervals de creixement i decreixement, si és còncava o convexa, els punts de tall (si n’hi ha) amb l’eix horitzontal i el punt de tall amb l’eix vertical, i una representació gràfica de la funció. |
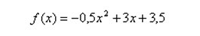 |
› › Clica per a veure el vídeo d’ACTIVITAT 259 › ›
| Aplicant el Teorema de Thales i les propietats dels triangles semblants, troba el valor dels segments: a, b, c, d |
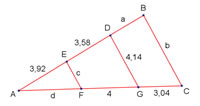 |
› › Clica per a veure el vídeo d’ACTIVITAT 258 › ›
Les piràmides de Kheops i Kefren són piràmides de base quadrada que tenen per amplada i altura respectivament: Kheops (230,35m ample, 146,6m altura) Kefren (215,25m ample i 143,5m altura).
1 – Calcula l’apotema lateral i l’aresta lateral de les piràmides
2 – Calcula la inclinació de la cara lateral
3 – Si la piràmide de Kefren tingués l’altura de la de Kheops (146,6m) però volguéssim que mantingués les proporcions originals quina hauria de ser la nova altura
4 – Si volguéssim que la piràmide de Kheops tingués les proporcions de la piàmide de Kefren però mantenint la seva amplada (230,35m) quina altura hauria de tenir |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 257 › ›
Troba la hipotenusa del triangle que té per catets 3 i 4
Troba el catet del triangle que té per hipotenusa 4,5 i l’altre catet val 2 |
|
› › Clica per a veure el vídeo d’ACTIVITAT 256 › ›
| Troba el valor que ha de tenir la hipotenusa d’un triangle si sabem que un catet és el doble de gran que l’altre. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 255 › ›
Comprova si els triangles que tenen per costats:
a) 5, 12, 13
b) 3, 4, 6
c) 4, 9, 9
són o no triangles rectangles |
|
› › Clica per a veure el vídeo d’ACTIVITAT 254 › ›
Tenim un pot de pilotes de tennis com el de la imatge, podem suposar que les pilotes ajusten perfectament (no hi ha espai lliure entre les pilotes i el lateral del cilindre, ni entre les pilotes i la base i la tapa).
Sabem que el diàmetre d’una pilota de tennis és de 6,2 cm.
Ens demanen que trobem, el volum del pot que no està ocupat per les pilotes |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 253 › ›
Raonament sobre la relació d’angles complementaris, suplementaris, oposats, i amb diferència de 90º i 180º
› › Clica per a veure el vídeo d’ACTIVITAT 252 › ›
|
|