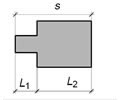
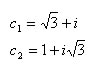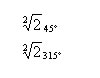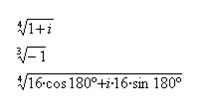PRoBLeMeS

ACTIVITAT 251

Exercici d’aplicació del Teorema de Thales

› › Clica per a veure el vídeo d’ACTIVITAT 251 › ›

ACTIVITAT 250

Les peces d’una màquina estan representades en un plànol. Una determinada peça de la màquina mesura 1,2 mm, però en el plànol aquesta longitud és de 15 cm. Ens demanen trobar l’escala del plànol.

› › Clica per a veure el vídeo d’ACTIVITAT 250 › ›

Desconeixem l’escala a la que està fet un plànol, en canvi sabem que la distància entre dos punts d’aquest plànol és de 3 cm i que a la realitat aquesta distància és de 15 Km. Es demana trobar l’escala d’aquest plànol.

› › Clica per a veure el vídeo d’ACTIVITAT 249 › ›

ACTIVITAT 248

› › Clica per a veure el vídeo d’ACTIVITAT 248 › ›

ACTIVITAT 247

Tenim un plànol a escala 1:1500000 que correspon a una determinada zona geogràfica. Sabem que la distànica entre dues ciutats d’aquesta zona és de 75 Km. Es demana trobar la distància equivalent al plànol

› › Clica per a veure el vídeo d’ACTIVITAT 247 › ›

ACTIVITAT 246

Multiplica i divideix entre si, els números complexos C1 i C2, tant en format binòmic com en format polar i comprova que els resultats obtinguts són els mateixos

› › Clica per a veure el vídeo d’ACTIVITAT 246 › ›

ACTIVITAT 245

Troba el número complex tal que el seu quadrat coincidexi amb el seu conjugat

› › Clica per a veure el vídeo d’ACTIVITAT 245 › ›

ACTIVITAT 244

Troba una equació de segon grau que tingui per solucions els números complexos que veus indicats a la pantalla

› › Clica per a veure el vídeo d’ACTIVITAT 244 › ›

ACTIVITAT 243

Calcula les arrels complexes que veus indicades a la pantalla

› › Clica per a veure el vídeo d’ACTIVITAT 243 › ›

ACTIVITAT 242

Calcula en forma binòmica i en forma polar (1 – i)⁵.

› › Clica per a veure el vídeo d’ACTIVITAT 242 › ›

ACTIVITAT 241

Operacions bàsiques amb números complexos: Suma , resta, multiplicació i divisió :
C1= 2 + 5i
C2= 3 – 4i

› › Clica per a veure el vídeo d’ACTIVITAT 241 › ›

ACTIVITAT 240

Calcula el volum i superfície total de l’envàs que veus a la imatge

› › Clica per a veure el vídeo d’ACTIVITAT 240 › ›

ACTIVITAT 239

Calcula el volum i superfície total d’una llauna de refresc com la de la imatge

› › Clica per a veure el vídeo d’ACTIVITAT 239 › ›

ACTIVITAT 238

Calculeu quantes taronges com les de la imatge calen per a obtenir 1 l de suc. (perímetre de la taronja pelada= 24cm)

› › Clica per a veure el vídeo d’ACTIVITAT 238 › ›

ACTIVITAT 237

Amb 200 m de filferro volem construir una tanca rectangular per a guardar el bestiar. Per tal de fer-la més gran aprofitarem la pared lateral de la masia, de manera que amb el filferro només caldrà fer 3 dels 4 costats, essent la paret el 4t costat.
Es demana trobar les dimensions del rectangle per tal d’obtenir la superfície màxima.

› › Clica per a veure el vídeo d’ACTIVITAT 237 › ›

ACTIVITAT 236

Un noi te una pilota a la mà, a l’alçada d’1 m. La llença verticalment amb una velocitat inicial de 20 m/s. (Considereu g= 10 m/s²)
1) Troba al cap de quant temps després de llençar la pilota, aquesta assolirà l’altura màxima
2) Quina serà l’altura màxima assolida
3) En quin instant arribarà la pilota al terra

› › Clica per a veure el vídeo d’ACTIVITAT 236 › ›

ACTIVITAT 235

Una ovella està lligada amb una corda de 5 m de longitud a un extrem d’un tancat en forma de triangle rectangle de costats 3, 4, 5 m que té uns angles de valor aproximadament: 53º, 37º i 90º.
Es demana la superfície de pastura que pot mejar l’ovella.

› › Clica per a veure el vídeo d’ACTIVITAT 235 › ›

ACTIVITAT 234

Calcula el volum i superfície lateral de la tassa que veus fotografiada

› › Clica per a veure el vídeo d’ACTIVITAT 234 › ›

ACTIVITAT 233

La funció de 2n grau – Aplicació de Geogebra
Amb aquesta aplicació es pot estudiar el comportament de la funció de 2n grau.
Es pot veure com evoluciona la seva forma, eix de simetria; les arrels, el punt de tall amb l’eix d’ordenades, vèrtex, i eventualment el màxim / mínim; tot depenent dels coeficients.

› › Clica per a veure el vídeo d’ACTIVITAT 233 › ›

ACTIVITAT 232

La funció afí (funció de 1r grau), propietats gràfiques – Aplicació Geogebra

En aquesta aplicació pots modificar el pendent de la recta, què és m, i l’ordenada a l’origen, que és n i observar com varia la recta

› › Clica per a veure el vídeo d’ACTIVITAT 232 › ›