| 5-Troba la derivada de la funció de la imatge. [Regla de la cadena] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 205 › ›
| 4-Troba la derivada de la funció de la imatge. [Regla de la cadena] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 204 › ›
| 3-Troba la derivada de la funció de la imatge. [Regla de la cadena] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 203 › ›
| 2 – Troba la derivada de funcions. Regla de la cadena. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 202 › ›
| [PAAU 2001]Els tres costats d’un triangle mesuren 3 cm, 4 cm i 5 cm . Calculeu els seus angles i la seva àrea. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 200 › ›
Troba el valor de la constant k perquè:
a) L’equació tingui 2 solucions
b) L’equació tingui 1 solució
c) L’equació no tingui solucions |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 199 › ›
| Resol el sistema de 3 equacions de 1r grau de la imatge |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 198 › ›
| Resol el sistema de dues equacions de segon grau amb dues incògnites al quadrat de la imatge |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 197 › ›
| Resol el sistema de dues equacions de segon grau amb dues incògnites al quadrat de la imatge |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 196 › ›
| [PAAU 1999] Una bola de 500 g que es deixa caure des d’una altura de 3 m sobre una superfície de sorra penetra 15 cm en la sorra abans d’aturar-se. Determina la força, suposada constant, de la sorra sobre la bola. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 194 › ›
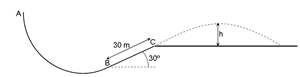
[PAAU 1999] Un esquiador de 80 kg que surt des de A arriba a B amb una velocitat de 30 m/s, i quan passa per C la seva velocitat és de 23 m/s. La distància entre B i C és de 30 m.
a) Quant han variat les energies cinètica i potencial de l’esquiador en anar des de B fins a C?
b) Quanta energia s’ha perdut per fregament en el tram recte BC? Quant val la força de fregament, suposada constant, en aquest tram?
c) Si la pista s’acaba a C i l’esquiador fa un salt parabòlic, quina és la màxima alçada h que assolirà, mesurada sobre el nivell de C (observa el dibuix)?
Suposa negligibles els efectes del fregament amb l’aire. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 193 › ›
[PAAU 1998] Un cos puja per un pla inclinat amb fregament per l’acció d’una força externa. Raona si és positiu, negatiu o nul el treball fet per les forces següents:
a) El pes.
b) La normal.
c) El fregament. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 192 › ›
[PAAU 2002] Una pilota de 5 kg de massa es llença des del terra verticalment cap amunt amb una velocitat inicial de 10 m/s. Si el vent comunica a la pilota una velocitat horitzontal constant de 15 km/h, trobeu:
a) L’alçada màxima a la qual arribarà la pilota i el temps que trigarà a assolir-la.
b) La distància entre el punt de llançament i el punt d’impacte amb el terra.
c) L’energia cinètica de la pilota en el moment d’impactar amb el terra. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 191 › ›
| [PAAU 2008] En la gràfica següent es mostra com varia l’acceleració d’un cos de massa 10 kg que es mou en línia recta. Quin treball s’ha efectuat sobre el cos per a moure’l des de x = 0 fins a x = 8 m? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 190 › ›
| [PAAU 1997] Un camió de 60 tones porta una velocitat de 72 km/h quan comença a frenar. Si s’atura 10 segons després, quina ha estat la potència mitjana de la frenada? (1 tona = 1000 kg) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 189 › ›
[PAAU 2009] El punt més alt d’una pista d’esquí (que podem aproximar a un pla inclinat sense fregament, tram AB), es troba a una altura h respecte del final. Fora de la pista, tram BC, no queda neu i per tant hi ha fregament (coeficient de fregament, μ, no nul). Si un esquiador surt del començament de la pista (punt A) a una velocitat nul·la:
1) Quina serà la seva velocitat al final de la pista (punt B)?
a) ARREL(2gh)
b) ARREL(gh/2)
c) Depèn de la massa de l’esquiador.
2) Quina distància horitzontal (BC) recorrerà l’esquiador abans d’aturar-se?
a) h·ARREL(μ)
b) h·μ
c) h/μ |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 188 › ›
|
|
