[PAAU 2002] Una pilota de 5 kg de massa es llença des del terra verticalment cap amunt amb una velocitat inicial de 10 m/s. Si el vent comunica a la pilota una velocitat horitzontal constant de 15 km/h, trobeu:
a) L’alçada màxima a la qual arribarà la pilota i el temps que trigarà a assolir-la.
b) La distància entre el punt de llançament i el punt d’impacte amb el terra.
c) L’energia cinètica de la pilota en el moment d’impactar amb el terra. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 191 › ›
| [PAAU 2008] En la gràfica següent es mostra com varia l’acceleració d’un cos de massa 10 kg que es mou en línia recta. Quin treball s’ha efectuat sobre el cos per a moure’l des de x = 0 fins a x = 8 m? |
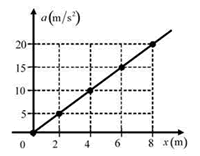 |
› › Clica per a veure el vídeo d’ACTIVITAT 190 › ›
| [PAAU 1997] Un camió de 60 tones porta una velocitat de 72 km/h quan comença a frenar. Si s’atura 10 segons després, quina ha estat la potència mitjana de la frenada? (1 tona = 1000 kg) |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 189 › ›
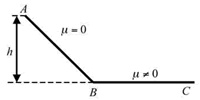
[PAAU 2009] El punt més alt d’una pista d’esquí (que podem aproximar a un pla inclinat sense fregament, tram AB), es troba a una altura h respecte del final. Fora de la pista, tram BC, no queda neu i per tant hi ha fregament (coeficient de fregament, μ, no nul). Si un esquiador surt del començament de la pista (punt A) a una velocitat nul·la:
1) Quina serà la seva velocitat al final de la pista (punt B)?
a) ARREL(2gh)
b) ARREL(gh/2)
c) Depèn de la massa de l’esquiador.
2) Quina distància horitzontal (BC) recorrerà l’esquiador abans d’aturar-se?
a) h·ARREL(μ)
b) h·μ
c) h/μ |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 188 › ›
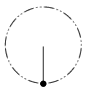
[PAAU 2003] Un cos de massa m lligat a l’extrem d’una corda de longitud L descriu una trajectòria circular de radi L en un pla vertical.
Quant val el treball realitzat per la tensió de la corda quan el cos va del punt més alt al punt més baix de la trajectòria?
Quant val el treball realitzat pel pes del cos entre aquests mateixos punts? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 187 › ›
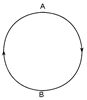
[PAAU 2000] Un avió de massa M fa un ris (loop) de manera que segueix una trajectòria circular i vertical de radi R.
a) Quin treball fa la força pes quan l’avió va del punt més alt A al punt més baix B de la trajectòria?
b) Quin treball fa aquesta força en fer una volta completa de A a B? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 186 › ›
| [PAAU 1998] Un nen de 30 kg es deixa caure per un tobogan de 2 m d’altura i arriba a terra amb una velocitat de 4 m/s. Quin treball han fet les forces de fregament? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 185 › ›
| [PAAU 1998] Un paracaigudista baixa a velocitat constant. Per tant, la seva energia cinètica es manté constant i la seva energia potencial disminueix. Significa, això, que no es conserva l’energia? Representa en un diagrama les forces que actuen sobre el paracaigudista i indica quina relació hi ha entre les forces |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 184 › ›
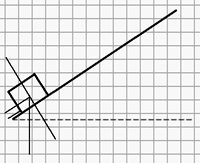
[PAAU 2008] Llancem cap amunt, amb una certa velocitat inicial, un cos de massa 1 kg per un pendent de 37° de manera que recorre 10 m fins a aturar-se i posteriorment torna al punt de partida. El coeficient de fricció entre el cos i el pla inclinat val 0,1.
1) El treball que fa el pes sobre la massa
a) és positiu a la pujada
b) val –59,0 J a la baixada
c) des que surt fins que torna al punt de partida (pujada i baixada) és nul.
2) El treball que fa la força de fricció sobre la massa
a) val –9,80 J a la pujada
b) val –7,83 J a la baixada
c) des que surt fins que torna al punt de partida (pujada i baixada) és nul. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 183 › ›
| Diferents activitats sobre probabilitat condicionada, lleis de Morgan, unió de probabilitats, diferència de processos … |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 182 › ›
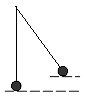
[PAAU 2009] Fem oscil·lar un objecte lligat a una corda de 40 cm de longitud, com si fos un pèndol, de manera que quan l’objecte es troba en el punt més alt de la trajectòria la corda forma un angle de 37° amb la vertical.
1) L’objecte passarà pel punt més baix del recorregut a una velocitat de
a) 2,50 m/s.
b) 2,80 m/s.
c) 1,26 m/s.
2) La tensió de la corda
a) és màxima en el punt més alt del recorregut.
b) és màxima en el punt més baix del recorregut.
c) fa un treball positiu sobre l’objecte quan passa del punt més alt al més baix de la trajectòria. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 181 › ›
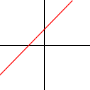
| Donada la recta y= 3x – 2, escriu la seva expressió en forma vectorial. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 180 › ›
| Donats els punts A(-2,-1) i B (1,5) troba l’equació de la recta que passa per aquests punts en forma: vectorial, paramètrica, continua, punt pendent, i explícita |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 179 › ›
| [PAAU 2000] És possible que un cos sobre el qual actua una única força de mòdul constant que forma un angle α≠0 amb la seva velocitat segueixi una trajectòria rectilínia? Raona la resposta. |
|
› › Clica per a veure el vídeo d’ACTIVITAT 178 › ›
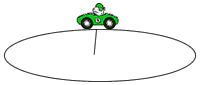
Un cotxe de massa 1.250 kg descriu un revolt circular, no peraltat, de 300 m de radi. La trajectòria és mitja circumferència. El cotxe augmenta de velocitat de manera uniforme mentre descriu el revolt, i passa d’anar a 40 km/h a l’inici a anar a 80 km/h al final. Calcula:
a) L’acceleració tangencial i l’acceleració centrípeta que té el cotxe quan circula a 20 m/s pel revolt.
b) El valor de la força de fricció estàtica entre les rodes i l’asfalt quan el cotxe circula a 20 m/s.
c) El valor del coeficient de fricció estàtica entre les rodes i l’asfalt si el cotxe pot circular pel revolt a una velocitat màxima de 30 m/s sense derrapar. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 177 › ›
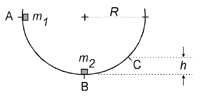
[PAAU 2004] Deixem caure un cos m1 de massa 1 kg des del punt A d’una guia semicircular de radi R = 2 m. En arribar al punt B, xoca contra una altra massa en repòs m2 de 500 g, de manera que després de l’impacte ambdues masses queden unides i el conjunt puja per la guia fins a una altura h de 60 cm (punt C). Sabent que en la meitat AB de la guia no hi ha fricció, però en l’altra meitat sí, calculeu:
a) La velocitat amb què m1 xoca contra m2.
b) El treball de la força de fricció en el tram BC.
c) La força que fa la guia sobre el conjunt en el punt C. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 176 › ›
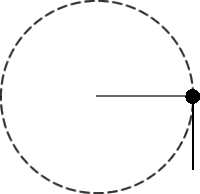
[PAAU 2004] Una partícula de massa 0,1 kg, lligada a l’extrem d’un fil, descriu un moviment circular en un pla vertical. Quan el fil es troba en posició horitzontal, la seva tensió és 10 N. Calcula per a aquesta posició:
a) L’acceleració centrípeta de la partícula.
b) L’acceleració tangencial de la partícula |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 175 › ›
[PAAU 2004] Un avió vola a una velocitat de mòdul 400 m/s, constant, i descriu un cercle en un pla horitzontal. Els límits de seguretat li permeten experimentar com a màxim una acceleració que és vuit vegades la de la gravetat. En aquestes condicions extremes, calcula:
a) El radi de la trajectòria circular.
b) El temps que l’avió triga a fer una volta.
c) L’angle d’inclinació de les ales de l’avió respecte de l’horitzontal perquè la força de sustentació (perpendicular al pla definit per les ales) li permeti fer aquest gir. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 174 › ›
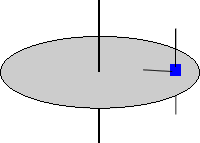
| [PAAU 2008] Una plataforma circular gira, en un pla horitzontal, respecte d’un eix vertical que passa pel seu centre, a una velocitat de 120/π rpm (revolucions per minut). Determineu el valor de la distància màxima respecte de l’eix a què pot situar-se una massa sobre la plataforma de manera que giri solidàriament amb aquesta, sense lliscar, sabent que el coeficient de fregament estàtic val 0,5. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 173 › ›
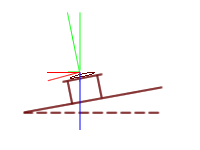
[PAAU 2007] En un tram del recorregut, l’AVE Lleida-Tarragona du una velocitat constant en mòdul de 300 km/h. En aquest tram fa un revolt de 600 m de radi que està peraltat amb un angle de 20º. Damunt d’una taula del vagó restaurant hi ha un plat buit de massa 350 g. El plat es troba en repòs en el tren gràcies a la fricció amb la taula, que impedeix que el plat es desplaci cap enfora.
a) Fes un diagrama de les forces que actuen sobre el plat.
b) Determina el mòdul de la força de fricció que actua sobre el plat.
c) Determina el mòdul de la força centrípeta que actua sobre el plat.
g= 10 m/s² |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 172 › ›
|
|

























