[PAAU 2001] Un mòbil que surt del repòs segueix una trajectòria circular de 3 m de radi amb una acceleració angular constant de Π rad/s²
a) Quant temps triga a fer una volta completa? Quina és la longitud de l’arc recorregut durant la meitat d’aquest temps?
b) Quina és la velocitat angular del mòbil a l’instant t= 0,5 s? I l’acceleració normal al mateix instant?
c) Quant val l’acceleració tangencial del mòbil a l’instant t= 0,5 s? Quin angle formen l’acceleració tangencial i l’acceleració normal en aquest instant? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 151 › ›
| [PAAU 2001] Una partícula surt del repòs i es mou sobre una recta. A la gràfica adjunta es representa l’acceleració de la partícula durant els 6 primers segons. Representa la gràfica v(t) del moviment |
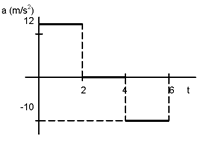 |
› › Clica per a veure el vídeo d’ACTIVITAT 150 › ›
| [PAAU 2002] El mòdul de la velocitat d’un punt material que descriu una trajectòria circular ve donat per l’equació (en unitats del SI) v= 6+10t. Si el radi de la trajectòria és de 100 m, quina serà l’acceleració normal en l’instant t= 8s. I l’acceleració tangencial? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 149 › ›
[PAAU 2004] En un moviment circular de radi r= 6.5 m, la velocitat angular ve donada per l’expressió ->2 + 3t (unitats SI)
a) Es tracta d’un MCUA? Per què?
b) Calcula l’acceleració tangencial i l’acceleració normal del punt mòbil en l’instant t= 3 s
c) Determina la longitud de l’arc recorregut en els dos primers segons del moviment
d) Troba la velocitat que agafa al final de la 1a volta |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 148 › ›
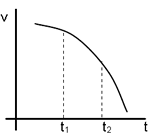
[PAAU 1998] El gràfic del costat està referit a un mòbil que descriu un moviment rectilini. Raona si les afirmacions següents són vertaderes o falses:
a) La gràfica correspon a un moviment uniformement accelerat
b) L’acceleració en el punt t1 és positiva i en el punt t2 és negativa |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 147 › ›
[PAAU 2002] Un mòbil que surt del repòs realitza un moviment circular accelerat uniformement. Raoneu si cadascuna de les afirmacions següents és certa o falsa:
a) El valor de l’acceleració normal del mòbil augmenta amb el temps
b) El valor de l’acceleració tangencial del mòbil no varia amb el temps |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 146 › ›
| [PAAU 1998] En un moviment curvilini l’acceleració forma, en un moment donat, un angle de 60º amb la velocitat i val 6 m/s². Calcula, per quest instant, el mòdul de les acceleracions tangencial i normal |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 145 › ›
| [PAAU 2001] Una partícula segueix una trajectòria circular de 3 m de radi. Si l’angle descrit ve donat per l’equació: angle= t² -1 on l’angle està expressat en radians i t en segons, quina és la longitud de l’arc recorregut entre els instants t= 1 s i t= 3 s? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 144 › ›
[PAAU 2000] Des d’una altura de 200 m sobre el terra llancem verticalment i cap amunt un cos amb una velocitat de 30 m/s.
a) Quant temps trigarà a recórrer els darrers 50 m?
b) Quina serà la seva posició respecte al terra a l’instant en que el cos baixa amb una velocitat de mòdul 40 m/s?
c) Feu un dibuix aproximat de la gràfica velocitat-temps corresponent al moviment d’aquest cos des de l’instant del llançament fins que arriba a terra.
Considereu g= 10 m/s² |
› › Clica per a veure el vídeo d’ACTIVITAT 143 › ›
| [PAAU 2004] La Lluna descriu una òrbita al voltant de la Terra que correspon pràcticament a un moviment circular uniforme de període T= 27,4 dies. La llum procedent de la Lluna triga 1,28 s a arribar a la Terra.
Calcula la velocitat angular i l’acceleració de la Lluna. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 142 › ›
[PAAU 2003] Una partícula segueix una trajectòria circular. Si l’angle descrit en funció del temps ve donat per l’expressió α= t², (en unitats del SI) calcula:
a) El temps que triga la partícula a fer les dues primeres voltes.
b) La velocitat angular de la partícula a t= s. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 141 › ›
[PAAU 1999] Un mòbil descriu un moviment circular de radi 2m. L’angle descrit pel mòbil en funció del temps ve donat per l’equació t³ + 5t – 4 (en unitats del SI). Calcula la expressió de la velocitat angular i l’acceleració tangencial per t=1s.
[Aquest és un Moviment Circular NO Uniformement Accelerat] |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 140 › ›
| Les dades de la taula corresponen a un cos que es mou amb MRUA. Acaba-la d’omplir |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 139 › ›
| [PAAU 2002] El mòdul de la velocitat d’un punt material que descriu una trajectòria circular ve donat per l’equació (en unitats del SI) v=6 + 10t. Si el radi de la trajectòria és de 100 m, quina serà l’acceleració normal quan t= 8 s? I l’acceleració tangencial? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 138 › ›
| [PAAU 1999] El rècord del món de salt d’altura està en 2,45 m. Es demana quina ha estat la velocitat inicial que ha fet l’atleta al iniciar el salt. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 137 › ›
| [PAAU 1999] D’una aixeta gotegen separades l’una de l’altra, dues gotes d’aigua. En un instant determinat, estan separades una distància d. Raona si, amb el pas del temps, mentre cauen, aquesta distància anirà augmentant, minvant o romandrà constant |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 136 › ›
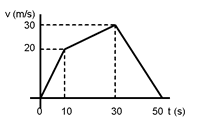
[PAAU 2001] La gràfica de la figura representa la velocitat en funció del temps d’un mòbil que surt de l’origen de coordenades i segueix un moviment rectilini. Calcula:
a) L’acceleració del mòbil a l’instant t= 20 s
b) La distància recorreguda durant el moviment de frenada
c) En quin interval de temps la seva acceleració és màxima? Dibuixa la gràfica x(t) per aquest interval |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 135 › ›
[PAAU 2002] Un coet és llançat verticalment cap amunt, des del repòs i puja amb una acceleració constant de 14,7 m/s² durant 8 s. En aquest moment se li acaba el combustible, i el coet continua el seu moviment de manera que l’única força a què està sotmès és la gravetat.
a) Calculeu l’altura màxima a què arriba el coet.
b) Calculeu el temps transcorregut des de la sortida fins a la tornada del coet a la superfície de la terra.
c) Feu un gràfic velocitat-temps d’aquest moviment |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 134 › ›
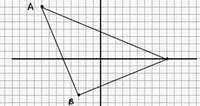
| Donats els punts A(-8,7), B(-3,-5), i C(9,0), que són els vèrtex d’un triangle i utilitzant vectors i les seves propietats, doneu tota la informació possible sobre aquest polígon. |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 133 › ›
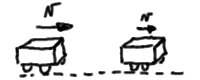
Un mòbil de massa 5 Kg i amb velocitat 10 m/s, persegueix un altre mòbil de massa 1 kg i velocitat 4 m/s. Xoquen i queden enganxats, movent-se en la mateixa direcció. Es demana
a) Amb quina velocitat es mou el conjunt?
b) Què ha passat amb l’energia cinètica? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 132 › ›
|
|



















