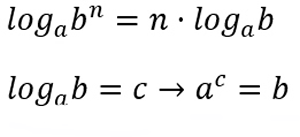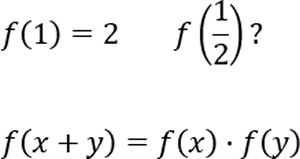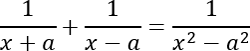[COMBINACIONS SENSE REPETICIÓ]
En un bloc de deu pisos, hem de pintar cada planta en blau o en groc, però dues plantes consecutives no es poden pintar de blau.
De quantes maneres diferents podríem pintar el bloc de pisos? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 593 › ›
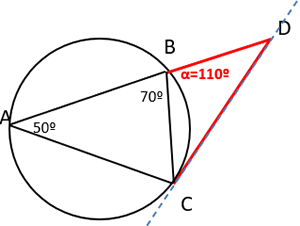
| Un triangle ABC amb A = 50º , B = 70º , està inscrit en un cercle.
La tangent a aquest cercle en el punt C talla la prolongació del costat AB al punt D.
Quant mesuren els angles del triangle BCD? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 592 › ›
Si log p19 = 20, troba log p2 191/2
Si log p a = 5 i log q a2 =12, troba log pq a3
Si log 2 10 = a, troba log10 2
Si log b a = c i log x b=c, troba log a x |
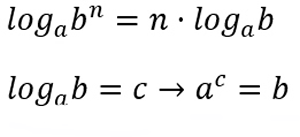 |
› › Clica per a veure el vídeo d’ACTIVITAT 591 › ›
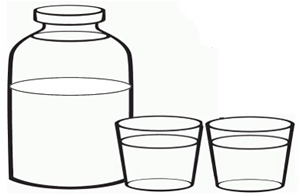
Amb les 3/4 parts de líquid que cap en una ampolla és pot omplir un got i mig.
Quants gots omplirem si tenim l’ampolla plena? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 590 › ›
[VARIACIONS SENSE REPETICIÓ i AMB REPETICIÓ]
Un parc té sis portes. La Mònica vol entrar i sortir.
a) De quantes maneres diferents ho pot fer, si no pot repetir porta al entrar i sortir?
b) I si pot entrar i sortir per la mateixa porta? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 589 › ›
| [COMBINACIONS SENSE REPETICIÓ]
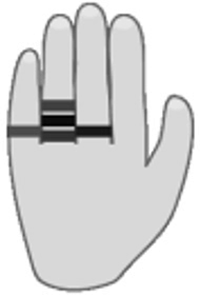
La Verònica es posa cinc anells tal com mostra la figura, i després se’ls treu d’un en un.
De quantes maneres diferents pot triar l’ordre en què se’ls treu? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 586 › ›
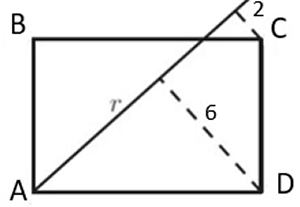
La recta r passa pel vèrtex A d’un rectangle ABCD. La distància des del punt C a la recta r és 2, i la distància des del punt D a la recta r és 6.
Si la longitud del costat AD és el doble que la del costat AB, quina és la longitud de AD? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 585 › ›
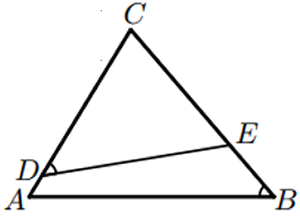
Les longituds dels costats d’un triangle △ABC són AB = 10, BC = 9 i CA = 8. El punt D és un punt del costat CA i compleix CD = 7 i el punt E és un punt del costat BC, de manera que els angles ABC i CDE són iguals.
Quin és el perímetre del triangle △CDE ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 584 › ›
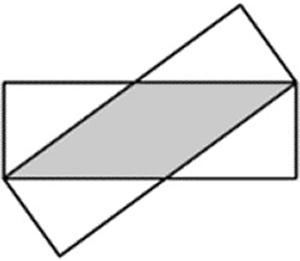
| Posem, un a sobre de l’altre, dos rectangles idèntics amb costats de 3 cm i 9 cm de longitud, com es mostra en la figura.
Quina és l’àrea de la intersecció dels dos rectangles? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 583 › ›
| Tots els valors que pren la funció f : R -> R són més grans o iguals que 0, i la funció f satisfà les condicions de la imatge,
Troba f(1/2). |
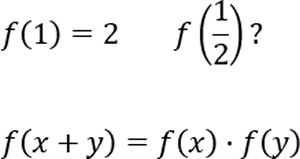 |
› › Clica per a veure el vídeo d’ACTIVITAT 582 › ›
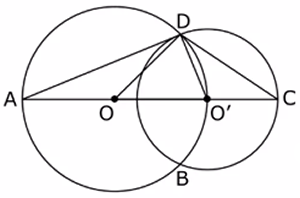
| DAC =20º, O i O’ són els centres de les circumferències.
Quant val ACD i ODO’ i ADC? ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 581 › ›
[PERMUTACIONS AMB REPETICIÓ]
Un partit d’hockey ha acabat 6-4.
De quantes maneres pot haver anat evolucionant el marcador fins arribar al final del partit? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 580 › ›
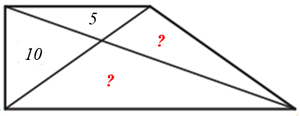
El quadrilàter de la imatge és un trapezi rectangle. Els nombres mostren les àrees de dos dels triangles interiors.
Quina és l’àrea del trapezi? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 579 › ›
| En un recipient hi ha 21 litres d’una dissolució que conté el 18% d’alcohol.
Traiem uns quants litres del líquid d’aquest recipient i els substituïm per una solució d’alcohol al 90%.
Si resulta una solució amb el 42% d’alcohol, quants litres hem tret i posat? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 578 › ›
Fins i tot quan un camell té set, el 84 % del seu pes és aigua. Després de beure, el seu pes augmenta fins a 800 kg i l’aigua constitueix el 85 % del seu pes.
Quant pesava, en kg, el camell abans de beure? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 577 › ›
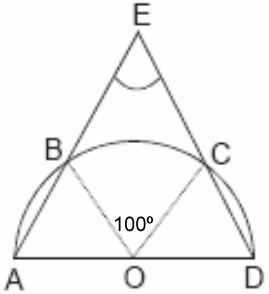
| A la semicircumferència de centre O de la figura, ∠ BOC fa 100º. △ AED és isòsceles.
Troba tots els angles |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 576 › ›
Si multipliquem per 3 els anys que jo tingui d’aquí a 3 anys i restem el triple dels que tenia fa 3 anys s’obtindran els anys que tinc ara.
Quina edat tinc ara? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 575 › ›
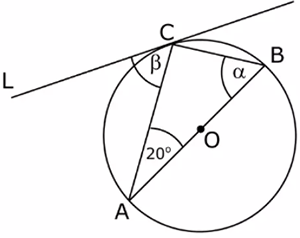
La recta L és tangent a la circumferència al punt on hi el vèrtex C del triangle,
quant val α i β |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 574 › ›
|
|