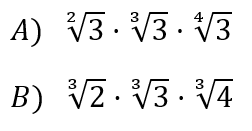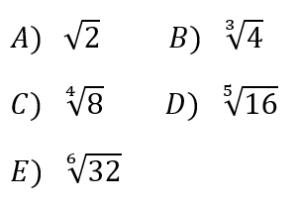| [PERMUTACIONS]En un prestatge, la Berta té tres diccionaris diferents i quatre novel·les, també diferents.
De quantes maneres pot col·locar aquests llibres si vol mantenir els diccionaris junts i les novel·les juntes també? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 531 › ›
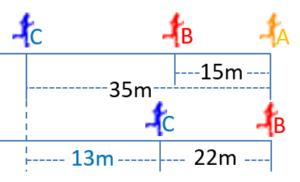
| L’Anna, en Bernat i en Carles corren una cursa. Surten junts i cadascú manté una velocitat constant. Quan l’Anna arriba al final, a en Bernat li falten 15 m per a acabar, i a en Carles, 35 m.
Quan en Bernat acaba, a en Carles li queden 22 m.
Quina és la longitud de la cursa? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 530 › ›
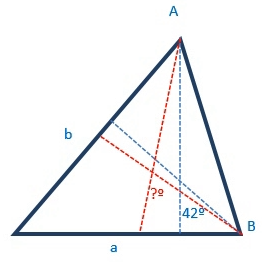
| L’angle que formen les altures corresponents als costats a i b d’un triangle acutangle △ABC mesura 42◦ .
Quant mesura l’angle que formen les bisectrius corresponents als vèrtexs A i B? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 526 › ›
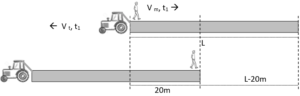
| En Marc va veure un tractor que arrossegava, a velocitat constant, un tub. Per tal de deduir quina era la longitud del tub, en Marc es va posar a caminar, també a velocitat constant, pel costat del tub. Primer va caminar en sentit contrari al del tractor i va haver de fer 20 passes per a anar d’una punta a l’altra. Després va caminar al costat del tub però en el mateix sentit que el tractor i va haver de fer 140 passes per a anar d’una punta a l’altra. Sabent que en Marc fa les passes d’1 m, quina és la longitud del tub? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 525 › ›
| L’Anna ha caminat 8 km a una velocitat de 4 km/h i a continuació es vol posar a córrer a una velocitat de 8 km/h.
Quant de temps ha de córrer per tal que la velocitat mitjana del trajecte sigui de 5 km/h? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 524 › ›
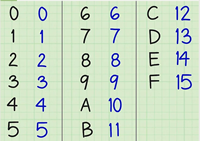
| Un estudiant ha escrit 14b · 25b = 416b. L’estudiant està calculant en base b i ha escrit l’expressió correctament.
Quina és la base b? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 523 › ›
| Els autobusos d’un aeroport surten cada 3 minuts cap al centre de la ciutat. Van per un carril reservat i tarden 35 minuts a arribar al centre. Un cotxe surt de l’aeroport al mateix temps que un autobús cap al centre i fa el mateix recorregut que el autobús però tarda 60 minuts. Sense comptar l’autobús que ha sortit al mateix temps que el cotxe, quants autobusos l’avançaran en el trajecte cap al centre? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 522 › ›
| Dos corredors s’entrenen en una pista circular de 720 metres. Els dos corren a velocitat constant en direccions oposades. El primer corredor triga quatre minuts a fer una volta completa i el segon triga cinc minuts.
Quants metres corre el segon corredor entre la primera i la segona vegada que es creuen? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 521 › ›
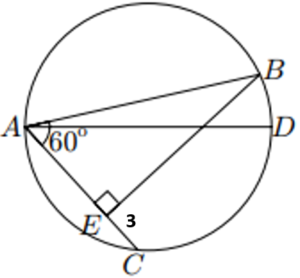
| En un cercle de diàmetre AD hem dibuixat dues cordes, AB i AC, de manera que BAC = 60º. Tracem BE perpendicular a AC i resulta que el segment EC fa 3 cm.
Quina és la longitud del segment BD (no dibuixat a la figura)? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 520 › ›
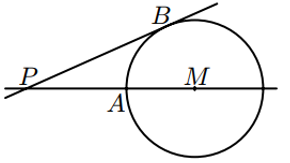
| A i B són dos punts d’una circumferència de centre M. El punt P és a la recta AM i la recta PB és tangent a la circumferència en el punt B. Les distàncies PA i MB són nombres enters i PB = PA + 6.
Quants valors diferents pot tenir el radi MB? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 519 › ›
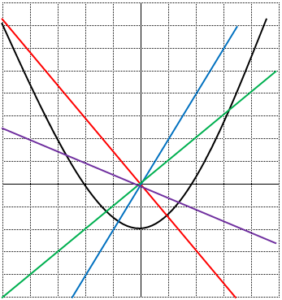
| Quatre línies rectes diferents passen per l’origen de coordenades. Les rectes intersequen la paràbola y = x2 − 2 en vuit punts.
Quin és el producte de les vuit coordenades x d’aquests punts? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 518 › ›
| Quants números compresos entre 210 i 213 són divisibles per 210? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 517 › ›
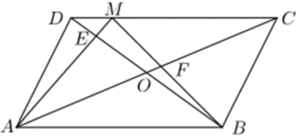
| La figura mostra un paral·lelogram ABCD d’àrea S. La intersecció de les diagonals del paral·lelogram és el punt O. El punt M es troba sobre el costat DC. La intersecció del segment AM amb la diagonal BD és el punt E i la intersecció del segment MB amb la diagonal AC és el punt F. La suma de les àrees dels triangles AED i BFC és S/3.
Quina és l’àrea del quadrilàter EOFM? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 516 › ›
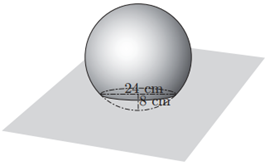
| Una pilota que estava flotant en un estany ha quedat enganxada quan aquest s’ha glaçat. En treure-la, ha quedat un clot en el gel de 24 cm de diàmetre i 8 cm de fondària.
Quin era el radi de la pilota? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 515 › ›
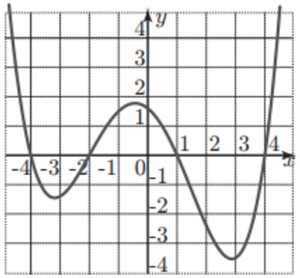
La figura mostra el gràfic d’una funció f : [−5; 5] → R.
Quantes solucions diferents té l’equació f(f(x)) = 0 ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 514 › ›
| Una successió numèrica té com a primer terme el nombre 1 i es compleix la propietat que, per a cada nombre natural n ≥ 2, la mitjana dels primers n termes de la successió és igual a n.
Quants termes hi ha estrictament més petits que 2021? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 513 › ›
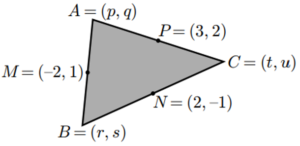
| Els tres vèrtexs d’un triangle són A = (p, q), B = (r, s) i C = (t, u), com es mostra a la figura. Els punts mitjans dels costats del triangle són els punts M = (−2, 1), N = (2, −1) i P = (3, 2).
Quin és el valor de p + q + r + s + t + u ? |
 |
› › Clica per a veure el vídeo d’ACTIVITAT 512 › ›
|
|